あるコンサート会場の入り口に開演前から行列ができています。また、一定の割合でこの行列に人が加わっています。入り口を５つ開けるとちょうど３０分で行列がなくなり、入り口を７つ開けるとちょうど１５分で行列がなくなります。ただし、「行列がなくなる」とは、新たに来た人が待たずに入り口を通れることを意味します。
(１) 行列がなくなるためには入り口はいくつ以上必要ですか。考えた過程も書きなさい。
(２) ちょうど１０分で行列がなくなるには入り口はいくつ開ければよいですか。
※ 解説を見たい場合は、下の「解説はこちらから」をクリック！
(１)
「入り口を５つ開けるとちょうど３０分で行列がなくなる」を図に表すと、次のようになります。
(画像はすべて、クリックすると拡大します)
同じように「入り口を７つ開けるとちょうど１５分で行列がなくなる」を図に表すと、次のようになります。
ひとつの入り口が１分間に通れる人数を[１]とおき、この２つの図を式で表す次のようになります。
【入り口を５つ開けたとき】
[１]×５か所×３０分＝[１５０]＝開演前の行列＋３０分で増えた人数
【入り口を７つ開けたとき】
[１]×７か所×１５分＝[１０５]＝開演前の行列＋１５分で増えた人数
そして、この２つの式を消去算のようにして計算すると、次の図のようになります。
１５分で増えた人数が[４５]なので、１分間で増える人数は[４５]÷１５＝[３]と表せます。
つまり行列をなくすためには、次の図のように毎分一定の割合で増え続ける
[３]の人数を通過させるための３つの入り口とは別に、開演前からならんでいた行列を通過させるための入り口(次の図の青色の点線の枠)が１つ以上必要になります。
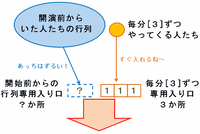
以上から、行列をなくすためには、入り口が最低でも３＋１＝４か所以上必要になります。
(２)
まずは開演前からならんでいた人数の割合を求めます。
さっきの問題で、１５分で増えた人数の割合は[４５]と表せることが分かったので、それを
「
[１０５]＝開演前の行列＋１５分で増えた人数の式」の式にあてはめると次のようになります。
つまり、
開演前からの行列である[６０]を１０分ですべて通過させるための入り口と、毎分[３]ずつ増える人たちを通過させるための入り口３つがあれば、１０分後には行列がなくなっているはずです(次の図)。
上の図の[６０]を１０分で通過させるためには、入り口が[６０]÷１０＝６か所必要です。
以上から、必要な入り口の数は全部で６＋３＝９か所になります。
PR
