水がいくらかたまっているタンクがあります。タンクの下には３本の排水管Ａ・Ｂ・Ｃがついていて、排水が始まると毎分一定の割合でタンクには水が加えられることになっています。排水管Ａは毎分５リットルの割合で、排水管Ｂは毎分６リットルの割合でタンクから排水することが分かっており、このタンクを空にするのに、排水管Ａだけを使うと１５分、排水管Ｂだけを使うと１０分かかります。このとき次の問いに答えなさい。
(１)
タンクには毎分何リットルの割合で水が加えられますか。
(２)
タンクの水を空にするのに、排水管Ｃだけを使ったときにかかる時間は、排水管ＡとＢを同時に使ったときにかかる時間よりも２５秒短くなります。このとき、排水管Ｃは毎分何リットルの割合でタンクの水を排水しますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
排水管Ａを１５分間使ったときに排出される水の量は５×１５＝７５リットルなので、「タンクに最初からたまっていた水」と「新たに１５分間でタンクへ追加された水」の合計は７５リットルです。
また、排水管Ｂを１０分間使ったときに排出される水の量は６×１０＝６０リットルなので、「タンクに最初からたまっていた水」と「新たに１０分間でタンクへ追加された水」の合計が６０リットルになります。
この２つの管から排出された水の量を次のような図に表して比べてみると、どちらも「タンクに最初からたまっていた水」の量は同じなので、排出された水の量の差である７５－６０＝１５リットルは、タンクへ新たに１５－１０＝５分間で追加された水にあたることが分かります。
※ 画像はすべて、クリックすると拡大します。
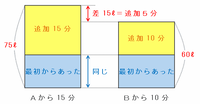
したがって、タンクへ１分間に追加される水の量は１５÷５＝３リットルになります。
(２)
さっきの問題で、タンクへ追加される水の量は毎分３リットルであることが分かったので、次は「タンクに最初からたまっていた水の量」を求めてみます。
次の図のように、排水管Ｂから１０分間で排出した６０リットルの水は、
・最初からタンクにたまっていた水
・新たに１０分間で追加された水
の２種類に分けることができます。
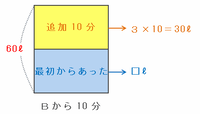
上の図の１０分間で追加された水の量は３×１０＝３０リットルなので、最初からタンクにたまっていた水の量は６０－３０＝３０リットルだと分かります。
また、排水管ＡとＢを同時に使うと、１分間で合わせて５＋６＝１１リットルの水が排出できます。
その毎分１１リットルの排出能力を、次の図のように
・毎分３リットルずつ追加される水を排出する係
・最初からたまっていた３０リットルを排出する係
に分けると、最初からたまっていた３０リットルが全部排出された瞬間に、タンクは空になります。
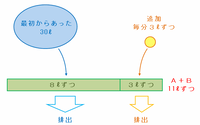
上の図の「最初からあった３０リットル」は１分間に１１－３＝８リットルずつ排出できるので、タンクが空になるまでにかかる時間は３０÷８＝３.７５分＝３分４５秒です。
排出管Ｃだけを使うとそれよりも２５秒早くタンクを空にできるので、そのときにかかる時間は３分４５秒－２５秒＝３分２０秒＝３分の１０分間です。
排出管Ｃがその時間でタンクから排出する水の量は、
・最初からタンクにたまっていた３０リットルの水
・毎分３リットルずつ３分の１０分間に追加された水→３×３分の１０＝１０リットル
の合わせて３０＋１０＝４０リットルの水なので、排出管Ｃが１分間に排出する水の量は、４０÷３分の１０＝１２リットルになります。
PR
