次の図のような直方体の形をした透明な水そうがあります。内側は、側面ＡＢＣＤに平行な長さ１０㎝の長方形の板ＰＱＲＳで図のように仕切られています。板ＰＱＲＳは、矢印の方向に毎分２㎝の速さで動くものとします。はじめは、水そうの色が塗られた①の部分に、体積５７６㎤の水が入っていて、このときの深さは４㎝です。次の問いに答えなさい。ただし、水そうと板の厚みは考えないものとします。
※ 画像はクリックすると拡大します。
(１)
初めのＱＢの長さは何㎝ですか。
(２)
水面がＰＳの線のところまで来るのは、板ＰＱＲＳが動き始めてから何分何秒後ですか。
(３)
板ＰＱＲＳが７分間動いたとき、②の部分の水の深さは何㎝ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図の仕切り板ＰＱＲＳの左側には５７６㎤の水が入っていて、その水の部分はたて８㎝、横□㎝、高さ４㎝の直方体になっています。
※ 画像はすべて、クリックすると拡大します。
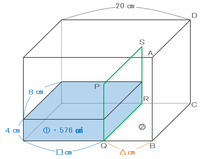
つまり、水の体積を求める式は８×□×４＝５７６㎤と表せるので、上の図の□には５７６÷８÷４＝１８㎝があてはまります。
直方体の容器の横の長さは２０㎝なので、最初のＱＢの長さ(上の図の△㎝)は２０－１８＝２㎝になります。
(２)
次の図のように、水面の高さが仕切り板の辺ＰＳの高さ(つまり１０㎝)まで来るとき、水の体積を求める式は８×□×１０＝５７６㎤と表すことができるので、下の図の□には５７６÷８÷１０＝７.２㎝があてはまります。
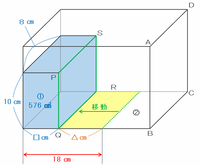
上の図のように、最初の仕切り板の位置は容器の左端から１８㎝、そして水面が辺ＰＳの高さまで来たときは仕切り板が容器の左端から７.２㎝の位置まで来るので、仕切り板は最初に比べて１８－７.２＝１０.８㎝動きました。
仕切り板は毎分２㎝の割合で左へ動くので、答えは１０.８÷２＝５.４分＝５分２４秒後になります。
(３)
最初の仕切り板の位置は容器の左端から１８㎝、そして板が７分間で動く距離は２×７＝１４㎝なので、７分後の板は次の図のように容器の左端から１８－１４＝４㎝の位置まで来ています。
また、容器の横の長さは２０㎝なので、板の右側にあたる辺ＱＢの長さは２０－４＝１６㎝になっていることも分かります。
上の図の①に入っている水の量は８×４×１０＝３２０㎤なので、残りの水の量である５７６－３２０＝２５６㎤は、仕切り板からあふれて右側の②へ流れ込みました。
このとき、②の部分に入っている水の体積を求める式は８×１６×□＝２５６㎤と表すことができるので、②の部分の水の深さは２５６÷８÷１６＝２㎝になります。
PR
