気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
06/15
Tue
2010
大妻2010【10】 ☆体積・容積☆
直方体の形をした空の容器A、B、Cがあります。Aは底面積が50㎠で深さが40㎝、Bは底面積が20㎠で深さが18㎝です。最初に、Aに深さ15㎝まで水を入れ、次にBを底面がAの底面にぴったりつくまで沈めていくと、図のように水の一部がBに入ってしまいました。
※ 画像はクリックすると拡大します。
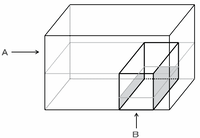
※ 画像はクリックすると拡大します。
(1)
Bに入っている水の深さは何㎝ですか。
(2)
Bを取り出し、Bに入っていた水を深さが25㎝のCに移します。CをAに沈めていくと、底面がAの底から3㎝のところで、AとCの水面の高さが同じになりました。Cの底面積は何㎠ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(1)
容器Bを入れる前のAを真正面から見ると、次の図のように底面積は50㎠、水の深さは15㎝なので、水の体積は50×15=750㎤です。
そのとき、容器Bに入っている水の深さは210÷20=10.5㎝になります。
(2)
その後、容器CをAの底面から3㎝の深さまで沈めたら、容器AとCの水面の高さが次の図のようにそろったのですが、この図は最初に750㎤の水を容器Aに入れたときの状態とまったく同じなので、水面の高さは容器Aの底から15㎝、そして容器Cの底からは15-3=12㎝になります。
つまり次の図のように、容器Cは水を210㎤入れると深さが12㎝になるので、底面積は210÷12=17.5㎤になります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
