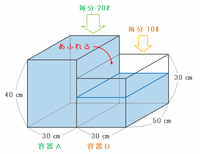
たて５０㎝、横９０㎝、高さ６０㎝の直方体の水そうに、次の図のようにすき間なく、３つの直方体の容器Ａ、Ｂ、Ｃを入れました。容器Ａに毎分２０リットル、容器Ｂに毎分１０リットルの水を同時に注ぎ始めます。次の問いに答えなさい。ただし、容器の厚さは考えないものとします。
※ 画像はすべて、クリックすると拡大します。
(１)
容器Ｂから水があふれるのは何分後でしょう。
(２)
容器Ｂの中に、上の図のように水の深さをはかるものさしを立てておきます。水を入れ始めてから、水そうの水がいっぱいになるまでの、時間と深さの関係のグラフを完成させなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
とりあえず、水が注ぎ込まれる容器ＡとＢの容積をそれぞれ求めてみると、
・容器Ａ→５０×３０×４０＝６００００㎤
・容器Ｂ→５０×３０×３０＝４５０００㎤
となります。
また、容器Ａには毎分２０リットル＝２００００㎤、容器Ｂには毎分１０リットル＝１００００㎤の水が入るので、計算上は
・容器Ａ→６００００÷２００００＝３分後に満水
・容器Ｂ→４５０００÷１００００＝４.５分後に満水
となるのですが、実際は次の図のように、２つの容器へ水を入れ始めてから３分後にはＡが満水となり、その後はＡからあふれた水がＢへと流れ込むため、Ｂは４.５分よりも早く満水になるはずです。
※ 画像はすべて、クリックすると拡大します。
２つの容器へ水を入れ始めてから３分後、容器Ｂには１００００×３＝３００００㎤の水が入ったので、満水まであと４５０００－３００００＝１５０００㎤です。
３分後からは、容器Ａからあふれた水がＢへ入ってくるので、容器Ｂには毎分２００００＋１００００＝３００００㎤の水が入ります。
１５０００÷３００００＝０.５分なので、容器Ｂが満水になるのは上の図から０.５分後、つまりスタートから３＋０.５＝３.５分後になります。
(２)
さっきの問題で、深さ３０㎝の容器Ｂが満水になるのは水を入れ始めてから３.５分後であることが分かったので、次のグラフのように「３分・２０㎝」から「３.５分・３０㎝」のところまで線が引けます。
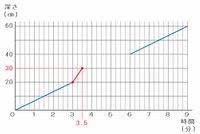
また、水の深さを測るものさしは容器Ｂの中に立っているので、次の図のように水が容器Ｂの右側へあふれ、その部分が容器Ｂの満水時の深さである３０㎝になるまではものさしのめもりが増えることはありません。
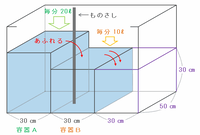
容器Ｂの右側にある深さ３０㎝分の容積は５０×３０×３０＝４５０００㎤であり、その部分に毎分２００００＋１００００＝３００００㎤の水が流れ込みます。
つまり、容器Ｂの右側の水深が３０㎝になるまでにかかる時間は４５０００÷３００００＝１.５分なので、次のグラフのように３.５＋１.５＝５分までは、水の深さが３０㎝のまま変わりません。
スタートから５分後、水面の高さは次の図のように容器Ａが４０㎝、そしてＡの右側は３０㎝になっています。
この図の状態から、Ａの右側の水面の高さが４０㎝になるまでは、水深が一定の割合で増えていきます。
上の図で、容器Ａの右側にあるすき間は、たて５０㎝、横３０×２＝６０㎝、高さ４０－３０＝１０㎝の直方体の形をしているので、その部分の容積は５０×６０×１０＝３００００㎤です。
その部分へ毎分３００００㎤の水が流れ込むので、上の図の状態から３００００÷３００００＝１分後には、水そう内部の水面の高さが４０㎝にそろいます。
つまり、スタートから５＋１＝６分後にはものさしのめもりが４０㎝をさしているので、次のグラフのように「５分・３０㎝」から「６分・４０㎝」のところまで線を引くとグラフが完成します。
PR
