太郎君と次郎君の１歩あたりの歩幅の比は３：４で、太郎君が４歩歩く時間と次郎君が５歩歩く時間は同じです。
(１)
太郎君と次郎君の速さの比を簡単な整数の比で表しなさい。
(２)
太郎君と次郎君が、ある動く歩道の上を歩きました。太郎君は２４歩で、次郎君は２０歩でそれぞれ渡りきりました。では、この動く歩道を太郎君が逆向きに歩くと何歩で渡りきりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
速さの比は「同じ時間に進む距離の比」と等しいので、太郎君が４歩、次郎君が５歩進んだ時の距離の比を求めればＯＫです。
２人の１歩あたりの歩幅の比は３：４なので、
・太郎君が４歩で進む距離→３×４＝１２
・次郎君が５歩で進む距離→４×５＝２０
と表せます。
したがって、２人が同じ時間に進む距離の比(つまり速さの比)は、太郎：次郎＝１２：２０＝３：５になります。
(２)
とりあえず、２人が動く歩道の上を進む場面をイメージしやすくするために、２人の歩幅や歩く時間に単位をつけて具体的な数に直してみます。
２人の歩幅の比は３：４なので、太郎君の１歩の長さは３ｍ、そして次郎君の１歩の長さは４ｍとします。
また、太郎君が４歩進む時間と次郎君が５歩進む時間は同じなので、その時間を２０秒とすると、
・太郎君が１歩進むのにかかる時間→２０秒÷４歩＝５秒
・次郎君が１歩進むのにかかる時間→２０秒÷５歩＝４秒
のように表せます。
太郎君は動く歩道を２４歩で進んだので、
・太郎君が自分の足で歩いて進んだ距離→３ｍ×２４歩＝７２ｍ
・太郎君が動く歩道を進むのにかかった時間→５秒×２４歩＝１２０秒
と表せます。
また、次郎君は動く歩道を２０歩で進んだので、
・次郎君が自分の足で歩いて進んだ距離→４ｍ×２０歩＝８０ｍ
・次郎君が動く歩道を進むのにかかった時間→４秒×２０歩＝８０秒
と表せます。
ただし、実際には２人が歩いているときに動く歩道自体も進んでいるので、動く歩道が１秒間にすすむ距離を１とおくと、
・太郎君が進むのにかかった１２０秒間に動く歩道が進んだ距離→１×１２０秒＝１２０
・次郎君が進むのにかかった８０秒間に動く歩道が進んだ距離→１×８０秒＝８０
と表せ、その距離を次の図のように２人が歩いた距離へそれぞれ加算すると、動く歩道の長さの図が完成します。
※ 画像はすべて、クリックすると拡大します。
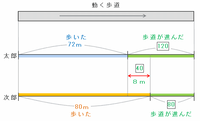
上の図のように、動く歩道の長さは
・太郎君が１２０秒間に歩いた７２ｍ＋歩道自体が１２０秒間で進んだ距離
・次郎君が８０秒間に歩いた８０ｍ＋歩道自体が８０秒間で進んだ距離
という２通りの表し方ができます。
つまり、歩道自体が１２０－８０＝４０秒間で進んだ距離は８０－７２＝８ｍなので、歩道自体が１秒間にすすむ距離は８÷４０＝０.２ｍ、そして歩道全体の長さは７２＋０.２×１２０＝９６ｍとなります。
※ 次郎君の進み方を利用して「８０＋０.２×８０＝９６ｍ」と求めてもＯＫ。
太郎君が１歩進む５秒間で、動く歩道は０.２×５＝１ｍ進みます。
次の図のように、太郎君が動く歩道の上を右から左へ逆向きに進むとき、
・太郎君→５秒間で１歩進み、右から左へ３ｍ動く
・動く歩道→５秒間で左から右へ１ｍ進み、その分だけ太郎君を押し戻す
ので、太郎君は１歩進むごとに３－１＝２ｍずつ移動します。
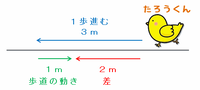
動く歩道の長さは９６ｍなので、太郎君は逆向きで９６÷２＝４８歩進んだときに渡りきります。
【補足】
この解説では１歩の歩幅を３ｍとか４ｍにしましたが、「いくらなんでも歩幅長すぎ(笑)」とか思った場合は、６０㎝と８０㎝ぐらいに置き換えればＯＫです。
また、「１歩進むのに４秒とか遅すぎでしょ(笑)」みたいに思った場合は、０.５秒と０.４秒、あるいは１秒と０.８秒ぐらいに置き換えればいいんじゃないでしょうか。
その分だけ計算がややこしくなったり、動く歩道の進む速さとの関係が複雑になるかもしれませんが、もちろんちゃんと正解にたどり着けるはずなのでがんばってください。
PR
