気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
08/05
Fri
2011
逗子開成2011【3】 ☆場合の数・4種類に色分けされた数字カードから3枚を選ぶ組み合わせ☆
赤、青、黄、緑の4色のカードが5枚ずつ計20枚あります。各色のカードには、それぞれ1から5までの整数が1つずつ書いてあります。この20枚のカードの中から、カードの色がすべて異なるように3枚のカードを選びます。このとき、次の選び方は何通りありますか。
(1)
3枚のカードの整数がすべて等しい場合。
(2)
3枚のカードの整数のうち、ちょうど2つが等しい場合
(3)
3枚のカードの整数のうち、最も小さい整数が4である場合
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(1)
たとえば「1」と書かれたカードは、次の図のように赤、青、黄、緑の4枚あるので、その中から3枚を選べばカードの整数がすべて「1」でそろいます。
※ 画像はすべて、クリックすると拡大します。
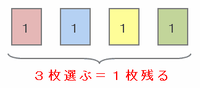
【同じ数をあてはめる2つの枠】
「4枚の中から3枚を選ぶ」ということは、逆の見方をすれば「4枚の中から使わない1枚を選ぶ」ことと同じので、「1」と書かれた4枚のカードから3枚を選ぶ方法は、
・赤いカードの「1」を選ばない
・青いカードの「1」を選ばない
・黄色いカードの「1」を選ばない
・緑色のカードの「1」を選ばない
の4通りになります。
また、「2」~「5」と書かれた4枚のカードについても、それぞれ3枚を選ぶ(というか1枚を選ばない)方法が4通りずつあるので、答えは4×5=20通りになります。
(2)
【同じ数をあてはめる2つの枠】
数字は「1」から「5」までのどれか1種類をあてはめるので、5通りの選び方があります。
また、色の選び方の組み合わせは、
・一方が赤→もう一方は「青・黄・緑」からどれか1つを選ぶので3通り
・一方が青→もう一方は「黄・緑」のどちらか1つを選ぶので2通り
・一方が黄→もう一方は緑しかないので1通り
となることから、全部で3+2+1=6通りあります。
つまり、数字の選び方は5通り、色の選び方の組み合わせは6通りなので、全部で5×6=30通りになります。
【違う数をあてはめる1つの枠】
【3つとも「4」を使う場合】
つまり、数字の選び方は5通り、色の選び方の組み合わせは6通りなので、全部で5×6=30通りになります。
【違う数をあてはめる1つの枠】
数字は「同じ数をあてはめる2つの枠」で使わなかった4種類からどれか1つを選ぶので4通り、色は「同じ数をあてはめる2つの枠」で使わなかった2種類のうちのどちらかなので2通りです。
したがって、数字と色の組み合わせは全部で4×2=8通りになります。
したがって、数字と色の組み合わせは全部で4×2=8通りになります。
以上から、「同じ数をあてはめる2つの枠」の数字と色の組み合わせは30通り、「違う数をあてはめる1つの枠」の数字と色の組み合わせは8通りあることが分かったので、3枚のカードの数字と色の組み合わせは全部で30×8=240通りになります。
【補足】
「同じ数をあてはめる2つの枠」について、色の選び方を
・1つ目の枠→「赤・青・黄・緑」のどれか1つを選ぶので4通り
・2つ目の枠→1つ目の枠で使わなかった3種類の中からどれか1つを選ぶので3通り
なので4×3=12通りじゃないの?と考えた瞬間にアウトです。
そのような数え方をするのは、たとえば「3枚のカードを並べて3けたの数を作る」とか「3枚のカードを選んで左から順に並べる」のような順番にこだわる問題の場合です。
今回のように「順番とかどうでもいいから、ただ単に3枚を選んでね」という問題の場合、たとえば「赤1・青1」と「青1・赤1」は1通りとして数えます。
(3)
3枚のカードのうち、最小の数を4にするには、「4」と「5」の2種類の数字だけ使えばOKなので、3つの数字の組み合わせは「3つとも4」、「4が2つと5が1つ」、「4が1つと5が2つ」の3パターンが考えられます。
【3つとも「4」を使う場合】
3つの数字をすべて4にするには、次の図の4色の「4」から「使わない1枚」を選べばOKなので、その選び方は4通りあります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
