床の上に、底面が１辺１２㎝の正方形で、深さが１８㎝の直方体の容器があり、その中にいくらか水が入っている。図のように、この容器を底面の辺の１つを床につけたままかたむけて水をこぼし、もとにもどした。かたむけた角度はま横から見て４５度で、こぼれた水の量は容積の１２分の１であった。容器の厚さは考えないものとして、以下の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
こぼれた水の量は何㎤ですか。
(２)
はじめに入っていた水の量は、容器の容積の何％ですか。
(３)
水をこぼしたあとの容器に、底面が１辺６㎝の正方形で、高さが１８㎝の直方体をまっすぐにしずめて立てた。その後、直方体を毎秒２㎝ずつまっすぐに引き上げていく。直方体が完全に水から引き上がるまでの間は、１秒間に水面が何㎝ずつ下がりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずはこの容器全体の容積から求めてみると、次の図のように底面は１辺１２㎝の正方形で高さは１８㎝なので、容積は１２×１２×１８＝２５９２㎤になります。
※ 画像はすべて、クリックすると拡大します。
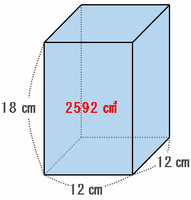
こぼれた水の量はその１２分の１なので、答えは２５９２÷１２＝２１６㎤になります。
(２)
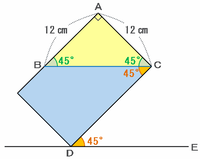
次の図のように傾いた状態の容器を真正面から見ると、角ＢＣＤの大きさは角ＣＤＥと等しい(錯角)ので４５度、角ＡＣＢの大きさは角ＡＣＤと角ＢＣＤとの差なので９０－４５＝４５度になります。
また、角ＢＡＣは直角、角ＡＢＣは１８０－(９０＋４５)＝４５度なので、三角形ＡＢＣは直角二等辺三角形になっています。
したがって、辺ＡＢの長さは辺ＡＣと同じく１２㎝です。
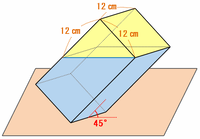
次の図の黄色い部分は、容器を傾けて水がこぼれた後にできたすきまを表しています。
その部分は三角柱(あるいは立方体の半分)になっているので、容積は１２×１２÷２×１２＝８６４㎤になります。
下の図の容器全体の容積は２５９２㎤、水がこぼれた後にできたすきまの容積は８６４㎤なので、残った水の量は２５９２－８６４＝１７２８㎤になります。
その容器にこぼれた水をすべて戻してあげると、水の量は１７２８＋２１６＝１９４４㎤に増えます。
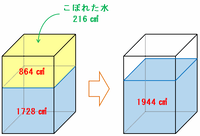
つまり、初めに入っていた水の量は１９４４㎤、そして容器全体の容積は２５９２㎤なので、答えは１９４４÷２５９２×１００＝７５％になります。
(３)
水の入った容器に突っ込む直方体の棒は、次の図のように底面が１辺６㎝の正方形になっているので、底面積は６×６＝３６㎠になります。
その棒を次の図のように水の中へ突っ込むと、容器の底面積は１４４－３６＝１０８㎠に減ります。
※ 水に入れた棒の分だけ底面積がせまくなる。
この問題は棒を２㎝持ち上げたときに水面が何㎝下がるのかを求めればＯＫなので、実際に棒を２㎝持ち上げて水面の変化を確かめてみます。
次の図のように棒を２㎝持ち上げると、棒の下にはオレンジ色のすきまができ、そこへ緑色の部分にあった水が流れ込んで水面が下がります。
※ 求めたいのは下の図の□㎝にあてはまる数です。
このとき、上の図の緑色２か所とオレンジ色の部分の容積は同じはずなので、どちらも「底面積×高さ」の答えは等しくなります。
オレンジ色の部分の容積は３６×２＝７２㎤、そして緑色の部分の容積を求める式は１０８×□＝７２㎤と表せるので、答え(□にあてはまる数)は７２÷１０８＝３分の２㎝になります。
PR
