○と×をいくつか並べるとき、×が２つ以上連続しない並べ方を考えます。例えば○と×を全部で２個並べるとき、条件を満たす並べ方は「○○」と「○×」と「×○」の３通りです。このとき、次の問いに答えなさい。
(１) ○と×を全部で３個並べるとき、条件を満たす並べ方は何通りになりますか。
(２) ○と×を全部で４個並べるとき、条件を満たす並べ方は何通りになりますか。
(３) ○と×を全部で１０個並べるとき、条件を満たす並べ方は何通りになりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
○と×を全部で３個並べる場合、次のように「○を３個使う」「○を２個使う」「○を１個使う」の３通りに場合分けして考えていきます。
・○を３個使う場合→「○○○」の１通りしかありません。
・○を２個使う場合→「×○○」「○×○」「×○○」の３通りあります。
・○を１個使う場合→「○×○」の１通りしかありません。
以上から、条件を満たす並べ方は全部で１＋３＋１＝５通りになります。
(２)
大きく分けて「○を４個」「○を３個」「○を２個」の３通りが考えられるので、さっきと同じように場合分けしてていねいに数えてみます。
【○を４個使う場合】
どう考えても「○○○○」の１通りしかありえません。
【○を３個使う場合】
次のＡからＤまでの４つのマスのうちのどれか１つに×をあてはめれば、残りの３つのマスは自動的にすべて○になるので、全部で４通りになります。
※ 画像はすべて、クリックすると拡大します。
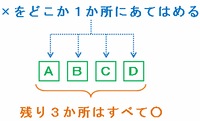
【○を２個使う場合】
○を２個使う場合は×も２個使うことになるので、まずは次の４つのマスに２個の×をとなり合わせにならないように並べ、その後で残り２つのマスに○をあてはめます。
上の図のＡからＤに２個の×をあてはめる方法は(Ａ・Ｃ)、(Ａ・Ｄ)、(Ｂ・Ｄ)の３組が考えられるので、この場合の並べ方は３通りになります。
以上から、○と×を４個使う場合、条件を満たす並べ方は全部で１＋４＋３＝８通りになります。
(３)
さっきと同じように「○を１０個」とか「○を９個」のように場合分けして数えても答えは求められるのですが、それはちょっと大変そうですよね。
というわけで、ここまでの流れを振り返って規則性を見つけてみると・・・
・○と×を合わせて２個使うとき→並べ方は全部で３通り
・○と×を合わせて３個使うとき→並べ方は全部で５通り
・○と×を合わせて４個使うとき→並べ方は全部で８通り
となっていることから、鋭い人はフィボナッチ数列のことを思い浮かべることができると思います。
フィボナッチ数列とは、たとえば「１→１→２→３→５→８」のように、前の２つの数の和が次の数になっている数列のことです。
実際に、○と×を４個使う場合の並べ方は、「２個使う場合の並べ方である３通り」と「３個使う場合の並べ方である５通り」の和である８通りになっています。
でもそれは単なる偶然かもしれないので(笑)、○と×を５個使う場合の並べ方が５＋８＝１３通りになっているかどうかを念のために確認してみます。
×が重ならないように○と×を合わせて５個並べる方法は、大きく分けて「○を５個」「○を４個」「○を３個」「○を２個」の４通りが考えられます。
このうち、○を５個使う場合は「○○○○○」の１通り、○を２個使う場合は「×○×○×」の１通りしかないので、あとは「○を４個」と「○を３個」の場合をそれぞれていねいに数えてみます。
【○を４個使う場合】
次のＡからＥまでの５つのマスのうちのどれか１つに×をあてはめれば、残りの４つのマスは自動的にすべて○になるので、全部で５通りになります。
【○を３個使う場合】
○を３個使う場合は×を２個使うことになるので、まずは次の５つのマスに２個の×をとなり合わせにならないように並べ、その後で残り３つのマスに○をあてはめます。
上の図のＡからＥに２個の×をあてはめる方法は(Ａ・Ｃ)、(Ａ・Ｄ)、(Ａ・Ｅ) 、(Ｂ・Ｄ)、(Ｂ・Ｅ)、(Ｃ・Ｅ)の６組が考えられるので、この場合の並べ方は６通りになります。
以上から、条件通りに○と×を合わせて５個並べる方法は、全部で１＋５＋６＋１＝１３通りとなり、次の図のようにフィボナッチ数列の考え方がピッタリあてはまることが確認できました。
フィボナッチ数列の規則に従って、上の図の続きを計算してみると・・・
・６個使う場合→８＋１３＝２１通り
・７個使う場合→１３＋２１＝３４通り
・８個使う場合→２１＋３４＝５５通り
・９個使う場合→３４＋５５＝８９通り
となるので、○と×を合わせて１０個使う場合の並べ方は、全部で５５＋８９＝１４４通りになります。
PR
