次の図のように、三角柱ＡＢＣの角Ｂが９０度の直角三角形を面にもつ三角柱の形の密閉された容器に水が入っています。この容器を面ＢＣＦＥが底面になるように置くと水の深さは２５㎝になりました。次の問いに答えなさい。ただし、容器の厚さは考えないものとします。
※ 画像はクリックすると拡大します。
(１)
面ＡＢＥＤが底面になるように置くと、水の深さは何㎝ですか。
(２)
辺ＢＥを床につけたまま水面が辺ＣＦと重なるようにかたむけました。水面と辺ＡＢが交わる点をＧとしたとき、ＡＧの長さは何㎝ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
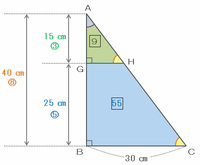
次の図の三角形ＡＧＨとＡＢＣは、角ＡＧＨとＧＢＣがともに直角で、角ＨＡＧは共通なので、内角の関係から相似であることが分かります。
また、辺ＡＧの長さは４０－２５＝１５㎝なので、三角形ＡＧＨとＡＢＣの長さの比はＡＧ：ＡＢ＝１５㎝：４０㎝＝３：８、そして三角形ＡＧＨとＡＢＣの面積比は３×３：８×８＝９：６４になります。
つまり、三角形ＡＧＨの面積は比の９、ＡＢＣの面積は比の６４なので、水にぬれた部分(台形ＧＢＣＨ)の面積は比の６４－９＝５５と表せます。
※ 画像はすべて、クリックすると拡大します。
次の図のように、三角柱の容器を面ＢＣＦＥが底面になるように(つまり辺ＢＥを軸として)傾けても、三角形ＡＢＣの中で水にぬれた部分の面積はさっきと変らないので、
・水にぬれた部分(台形ＰＡＢＱ)の面積→比の５５
・上部にできたすきま(三角形ＰＱＣ)の面積→比の９
・三角形ＡＢＣの面積→比の５５＋９＝６４
と表せます。
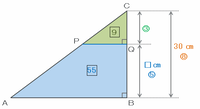
また、上の図の三角形ＰＱＣとＡＢＣは内角の関係から相似だと分かるので、面積比がＰＱＣ：ＡＢＣ＝９：６４＝３×３：８×８なら、長さの比はＰＱＣ：ＡＢＣ＝３：８になります。
つまり、上の図の辺ＣＢの長さは比の８、辺ＣＱの長さは比の３にあたるので、辺ＱＢの長さ(つまり水面の高さ)は比の８－３＝５と表せます。
比の８が３０㎝なので、比の１は３０÷８＝３.７５㎝、そして水面の高さである比の５は３.７５×５＝１８.７５㎝になります。
(２)
三角柱の容器を、次の図のように水面の右側が点Ｃへ来るまで傾けたときも、上部にできたすきま(三角形ＣＡＧ)の面積は比の９、そして水にぬれた部分(三角形ＣＧＢ)の面積は比の５５です。
また、三角形ＣＡＧの底辺をＡＧ、三角形ＣＧＢの底辺をＧＢとすると、高さはどちらも辺ＣＢになるので、この２つの三角形の底辺比は面積比と同じく９：５５になります。
つまり、上の図の辺ＡＢの長さである４０㎝を９：５５に比例配分すれば、辺ＡＧの長さが求められるので、答えは４０×６４分の９＝５.６２５㎝になります。
【追記】
最初に水の容積を求めてからうにゃうにゃと求める方法でもいけるんだけど、「容器を同じ軸で傾けてる限り、水にぬれた部分の面積は変わらない」という視点から解いた方が圧倒的に楽だと思います。
PR
