中学生のグループと高校生のグループが、体育館と廊下を掃除します。中学生のグループが体育館だけを掃除すると３０分かかり、廊下だけを掃除すると５０分かかります。高校生のグループが体育館だけを掃除すると６０分かかります。また、同じ時間で１人の生徒ができる仕事の量は、中学生は高校生の０.７倍です。次の問いに答えなさい。
(１)
高校生のグループが廊下だけを掃除すると、何分かかりますか。
(２)
中学生のグループの人数と高校生のグループの人数の比を求めなさい。
(３)
中学生のグループが体育館だけを掃除し、高校生のグループが廊下だけを掃除することになりました。２か所の掃除を同時に終わらせるため、中学生のグループから３５人を高校生のグループに移動させました。高校生の人数を求めなさい。また、掃除を終わらせるには何分何秒かかりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
体育館の掃除にかかった時間を比べてみると、高校生グループは中学生グループの６０÷３０＝２倍になっています。
つまり、廊下を掃除するのにかかる時間も、高校生グループは中学生グループの２倍になるはずなので、答えは５０×２＝１００分です。
(２)
同じ時間で１人の生徒ができる仕事の量は、中学生は高校生の０.７倍なので、その関係を比で表すと中学生：高校生＝０.７：１＝７：１０になります。
中学生グループの人数を□人、高校生グループの人数を△人とおき、それぞれのグループが体育館を掃除した場面を式で表すと、
・中学生グループ→７×□人×３０分＝２１０×□人
・高校生グループ→１０×△人×６０分＝６００×△人
となります。
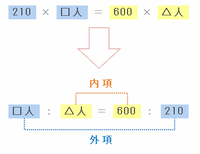
その「２１０×□人」と「６００×△人」の答えは同じなので、次の図のように「比の内項と外項の積は等しい」ことを利用して、□人と△人の比を求めてみると、□人：△人＝６００：２１０＝２０：７となります。
※ 画像はすべて、クリックすると拡大します。
(３)
これまでの問題で、中学生グループと高校生グループの仕事量の比は７：１０、人数の比は２０：７であることが分かったので、体育館を掃除するのに必要な仕事量(中学生グループなら３０分)は７×２０×３０分＝４２００、そして廊下を掃除するのに必要な仕事量(中学生グループなら５０分)は７×２０×５０分＝７０００と表せます。
つまり、体育館と廊下を掃除するのに必要な仕事量の比は４２００：７０００＝３：５なので、中学生と高校生の仕事量の合計を３：５に比例配分すれば、２か所の掃除が同時に終わります。
中学生グループの１分間の仕事量は７×２０＝１４０、高校生グループの１分間の仕事量は１０×７＝７０なので、この２つのグループの仕事量全体は１４０＋７０＝２１０と表せます。
その仕事量を体育館：廊下＝３：５に比例配分すればＯＫなので、
・体育館掃除担当の１分間あたりの仕事量→２１０×８分の３＝７８.７５
・廊下掃除担当の１分間あたりの仕事量→２１０×８分の５＝１３１.２５
のように仕事能力を振り分けます(次の図参照)。
上の図で体育館掃除と廊下掃除にかかる時間は同じなので、とりあえず体育館掃除にかかる時間を求めてみると、４２００÷７８.７５＝５３と３分の１分間＝５３分２０秒になります。
※ 廊下掃除にかかる時間は７０００÷１３１.２５＝５３と３分の１分間＝５３分２０秒。当たり前だけど体育館掃除にかかる時間と同じなので、どちらで求めてもＯＫです。
また、上の図で体育館掃除に振り分けた仕事量である７８.７５は、３５人が抜けた後の中学生グループの仕事量を表しています。
次の図のように、もともとの中学生グループの仕事量は７×２０＝１４０、３５人が抜けた後の中学生グループの仕事量は７８.７５なので、３５人分の仕事量は１４０－７８.７５＝６１．２５になります。
６１.２５÷１４０＝０.４３７５なので、中学生グループの０.４３７５が３５人にあたることが分かります。
つまり、中学生グループは３５÷０.４３７５＝８０人、そして中学生グループと高校生グループの人数比は２０：７なので、高校生グループの人数を□人とおくと、２０：７＝８０人：□人という比例式ができます。
以上から、高校生の人数は７×８０÷２０＝２８人になります。
PR
