気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
05/27
Fri
2011
東海2011【2】 ☆容積・容器を傾けた後に残った水の量を求める☆
次の図1のような容器があります。この容器の2つの面は直角二等辺三角形と正方形を組み合わせた形で、他の面はすべて長方形です。この中に、深さが6分の5になるまで水を入れました。
(1)
この容器を真正面から見ると、三角形AIFは直角二等辺三角形なので、角HABとGFEはどちらも45度です。
また、角AHBとFGEは直角、角ABHとFEGは180-(45+90)=45度なので、三角形ABHとFEGはどちらも直角二等辺三角形です。
上の図の辺HGはCDと同じく8㎝、辺AFは16㎝なので、辺AHとGFの長さはどちらも(16-8)÷2=4㎝です。
また、三角形ABHとFEGはどちらも直角二等辺三角形であり、辺AHとHB、辺GFとGEの長さはそれぞれ等しいので、辺HBとGEの長さも4㎝です。
つまり次の図のように、容器全体の高さはHB+BC=4+8=12㎝、そして水面の高さは容器全体の6分の5なので12×6分の5=10㎝になります。
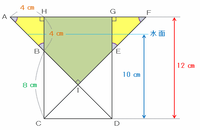
次の図のように、水面の高さは底面から10㎝なので、水面から容器のてっぺんまでは12-10=2㎝です。
つまり、下の図の辺HLとGMは2㎝、辺HBとGEは4㎝なので、辺LBとMEはどちらも4-2=2㎝です。
また、JBLとKEMも直角二等辺三角形なので、辺JLとMKの長さはどちらも2㎝になります。
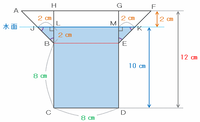
つまり、上の図の辺JKの長さはJL+LM+MK=2+8+2=12㎝なので、赤い点線BEの下と上にある水面の面積は、
・赤い点線の下(正方形BCDE)→8×8=64㎠
・赤い点線の上(台形JBEK)→(12+8)×2÷2=20㎠
となります。
したがって、次の図のように容器を真正面から見たとき、水の入った部分の面積は64+20=84㎠になります。
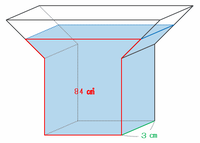
上の図の辺ACとBEは平行なので、角ACBとEBCの大きさは同じです(錯角の関係)。
したがって、次の図のように容器を真正面から見たとき、水の入った部分の面積は64+20=84㎠になります。
上の図で水が入っている部分の立体は、底面を赤い線で囲ったY字っぽい部分とすると、高さは緑色の3㎝の部分とみなすことができるので、水の体積は84×3=252㎤になります。
(2)
次の図のように、辺BCを右側へ伸ばすと直角二等辺三角形CDEができ、辺CDとDEの長さはどちらも4㎝になります。
上の図の辺ACとBEは平行なので、角ACBとEBCの大きさは同じです(錯角の関係)。
また、角ADCとEDCはどちらも直角なので、三角形ABCとEDBは2つの内角の大きさが(そして残りの1つの角の大きさも)等しいことが分かります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
