あき子さんと兄が家から同じ道をポストに向かってそれぞれ一定の速さで歩いていきます。８時にあき子さんはポストまで３５７ｍの地点にいて、兄の６３ｍ前方にいました。兄は８時３分にあき子さんを追い越し、８時５分にポストに着いて、すぐに同じ道を引き返しました。兄があき子さんと出会うのはポストから( )ｍの地点です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
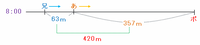
８時ちょうどのときの位置関係を次の図のように表してみると、あき子さんはポストまで３５７ｍ、そして兄はあき子さんまで６３ｍの地点にいるので、兄とポストとの間の距離は３５７＋６３＝４２０ｍです。
※ 画像はすべて、クリックすると拡大します。
兄がポストに着くのは８時５分なので、次の図のように、兄はポストまでの４２０ｍを５分間で進みます。
つまり、兄が進む速さは４２０÷５＝分速８４ｍです。
次の図のように、兄はあき子さんに追いつくまでの３分間で８４×３＝２５２ｍ進むので、あき子さんがその３分間で進んだ距離は、２５２－６３＝１８９ｍです。
つまり、あき子さんが進む速さは１８９÷３＝分速６３ｍです。
８時ちょうどから８時５分までの５分間で、あき子さんは６３×５＝３１５ｍ進みます。
したがって、８時５分にポストへ着いた兄が引き返し始めるとき、２人の間の距離は次の図のように３５７－３１５＝４２ｍ離れています。
２人が上の図の４２ｍを向かい合わせで進んで出会うまでにかかる時間は、４２÷(６３＋８４)＝７分の２分間です。
求めたいのは、兄が７分の２分間でポストから進んだ距離なので、答えは８４×７分の２＝２４ｍになります。
【補足】
２人の進む速さは、あき子：兄＝分速６３ｍ：分速８４ｍ＝３：４なので、次の図のように４２ｍを３：４に比例配分すれば、出会うまでに２人がそれぞれ進んだ距離を求めることができます。
PR
