公園に大きなデジタル時計があります。この時計は０：００から２３：５９の２４時間表示です。１５時３分は次の図１のように、６時３０分は図２のように表示されます。
※ 画像はすべて、クリックすると拡大します。
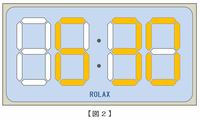
この時計のひとつひとつの数字は、図３の７本のライトに電気がついて表示され、このライト１本を１分間つけるのに必要な電気代は１円です。０から９までの数字の表示方法と１分間の電気代は下の表１の通りです。時と分の間にある２つの点「：」の電気代は考えません。
０：００からの５分間は、０：００が表示されはじめてから０：０４の表示が終わるまでとして、次の( )をうめなさい。
(１) ６：３０からの１０分間にかかる電気代は( )円です。
(２) ( ： )からの１０分間にかかる電気代が一番高くなります。
(３) １１：( )からの５分間にかかる電気代は６０円です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
６時３０分から１０分間のデジタル時計は、次の図のように「６時」の「６」と「３□分」の「３」はどちらも１０分間そのまま表示され、分の一の位は「０」から「９」が１分ごとに入れ替わります。
※ 画像はすべて、クリックすると拡大します。
上の図の「６」が１０分間表示されたときの電気代は６×１０＝６０円、「３」が１０分間表示されたときの電気代は５×１０＝５０円になります。
また、分の一の位に「０」から「９」が１分ずつ表示されたときの電気代は、６＋２＋５＋５＋４＋５＋６＋４＋７＋５＝４９円です。
以上から、６時３０分から１０分間の電気代の合計は、６０＋５０＋４９＝１５９円になります。
(２)
デジタル時計の「○△時」の部分には「０」から「２３」までのどれかがあてはまるのですが・・・
・「○」が１の場合→△に「８」をあてはめて「１８時」にしたとき、１分間の電気代は２＋７＝９円
・「○」が２の場合→△に「０」をあてはめて「２０時」にしたとき、１分間の電気代は５＋６＝１１円
となるため、下の図の「：」の左側には「２０」があてはまります。
上の図の「分」にあてはまる２つの数のうち、十の位には「０」から「５」までのうちのどれかが表示されるのですが、その中でいちばん電気代が高くなる数字は「０」なので、十の位は「０」で決定です。
最後に「分」の一の位について考えてみると、十の位にある「０」をなるべく長く表示させるためには、一の位に「０」をあてはめればＯＫなので、一の位も「０」で決定です。
※ ００分から０９分が終わるまで、十の位には「０」が表示され続ける。
以上から、１０分間の電気代がいちばん高くなるのは「２０：００」からの１０分間になります。
(３)
簡単に言うと、電気代がちょうど６０円になる５分間を意地と気合と根性で見つければそれでおしまいです(笑)
でも、それだと運任せのがむしゃらな作業になってしまうので、少しぐらいはスマートに答えを求めてみたいと思います。
この問題は「○△時」の部分に「１１時」があてはまることは確定しているので、その部分の電気代は５分間で(２＋２)×５＝２０円になります。
電気代の合計は６０円なので、「○△分」の部分の５分間の電気代は６０－２０＝４０円になます。
このとき、下の図の青色と緑色の部分にあてはまる数の特徴を確認してみると・・・
・青色の部分→「分」の十の位なので、「０」から「５」までのどれかがあてはまる。
・緑色の部分→「分」の一の位なので、５分間で連続した５つの数が入れ替わる。
のようになっています。
また、緑色の部分の５分間の電気代が最も安くなるように連続する５つの整数を選んでみると、それは「１」から「５」を使った場合の２＋５＋５＋４＋５＝２１円であることが分かります。
つまり、青色の部分の電気代は５分間で４０－２１＝１９円を超えたらアウトなのですが、「０」から「５」の中でその条件にあてはまるのは、１分間の電気代が２円である「１」のときしかありません。
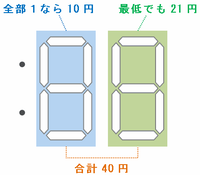
というわけで、「分」の十の位には「１」があてはまります、と言いたいところなのですが、実際には次の図のように、
① ５分間がすべて「１○分」の場合
② 最初の数分間は「０△分」で、その続きが「１○分」の場合
③ 最初の数分間は「１○分」で、その続きが「２△分」の場合
という３つの可能性が考えられます。
【補足】
上の図で「２２」までしか考えないのは、十の位で「２」を４個も使った時点で電気代が５×４＝２０円になり、「十の位の電気代は５分間で１９円以下」の条件を満たさなくなるからです。
また、十の位に「０」を３個使っただけで電気代が６×３＝１８円となってしまうので、「０７」よりも前の部分を範囲として考える必要はないことが分かります。
【可能性① ５分間がすべて「１○分」の場合】
５分間がすべて「１○分」の場合、とりあえず十の位で「１」を５分間使うので、その分の電気代が２×５＝１０円になります。
十の位と一の位の電気代の合計は４０円なので、残りの４０－１０＝３０円は一の位の電気代になります。
このとき、連続する５つの数を一の位に使ってちょうど３０円になる場合があるかどうかを次の表で確かめてみると、残念ながらそれにあてはまるケースが見当たりません。
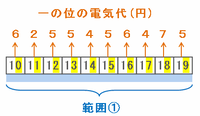
【可能性② ５分間の前半は「０△分」の場合】
５分間の前半が「０△分」の場合、下の範囲②の中から、連続する５個の整数を使うことになります。
とりあえず下の図の中央辺りにある「０９」「１０」「１１」の１分間の電気代をそれぞれ求めてみると・・・
・「０９」→「０」は６円、「９」は５円なので、６＋５＝１１円
・「１０」→「１」は２円、「０」は６円なので、２＋６＝８円
・「１１」→「１」は２円なので、２＋２＝４円
となり、この３つの数の電気代は１１＋８＋４＝２３円となることが分かります。
このとき、残りあと２つの数の電気代は４０－２３＝１７円になるので、その組み合わせがあるかどうかを調べてみると・・・
・「０７」と「０８」の場合→電気代の合計は６＋４＋６＋７＝２３円
・「０８」と「１２」の場合→電気代の合計は６＋７＋２＋５＝２０円
・「１２」と「１３」の場合→電気代の合計は２＋５＋２＋５＝１４円
となることから、残念ながら可能性②も正しくないことが分かります。
【可能性③ ５分間の前半は「１△分」の場合】
５分間の前半が「１△分」の場合、下の範囲③の中から、連続する５個の整数を使うことになります。
さっきと同じように下の図の中央辺りにある「１８」「１９」「２０」の１分間の電気代をそれぞれ求めてみると・・・
・「１８」→「１」は２円、「８」は７円なので、２＋７＝９円
・「１９」→「１」は２円、「９」は５円なので、２＋５＝７円
・「２０」→「２」は５円、「０」は６円なので、５＋６＝１１円
となり、この３つの数の電気代は９＋７＋１１＝２７円となることが分かります。
このとき、残りあと２つの数の電気代は４０－２７＝１３円になるので、その組み合わせがあるかどうかを調べてみると・・・
・「１６」と「１７」の場合→電気代の合計は２＋６＋２＋４＝１４円
・「１７」と「２１」の場合→電気代の合計は２＋４＋５＋２＝１３円→あったぞー！
・「２１」と「２２」の場合→電気代の合計は５＋２＋５＋５＝１７円
となることから、「１７分」から「２１分」までの５分間なら、問題文の条件にピッタリあてはまることが分かります。
以上から、答えは「１７」になります。
PR
