水がいっぱいに入った直方体の形をした水そうの中に、一辺の長さが６㎝の正方形を底面とする直方体の柱が図１のように立っています。
柱を３.２㎝持ち上げたら、水面が０.８㎝下がりました。図２はこの様子を表しています。次に、図３のように、イの長さが図２のアの長さの７分の２倍となるように柱を持ち上げたら、水面がさらに１.２㎝下がりました。
次の問いに答えなさい。(式や考え方も書きなさい)
※ 画像はクリックすると拡大します。
(１) 水そうの底面積は何㎠ですか。
(２) 水そうの深さは何㎝ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
直方体の柱を３.２㎝持ち上げることによって、柱の下には次の図のようにオレンジ色のすきまができます。
そこに緑色の部分にあった水が流れ込むため、水面は０.８㎝下がります。
※ 画像はすべて、クリックすると拡大します。
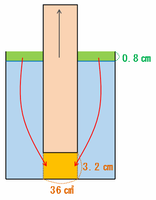
このとき、緑色２か所の体積とオレンジ色の部分の体積は同じはずなので、次のどちらの図も「底面積×高さ」の答えは等しくなります。
また、緑色２か所とオレンジ色の高さの比は０.８㎝：３.２㎝＝１：４なので、底面積の比をその逆の４：１にしてやれば、２つの立体の体積は同じになります。
上の図から、緑色２か所の立体の底面積は３６×４＝１４４㎠と分かるのですが、この容器自体の底面積は緑色２か所とオレンジ色の部分を合計すれば求められるので、答えは３６＋１４４＝１８０㎠になります。
(２)
次の図Ａから図Ｂのように、アの７分の５を持ち上げることによって水面は１.２㎝下がります。
つまりアの７分の１を持ち上げるごとに水面は１.２÷５＝０.２４㎝ずつ下がるので、下の図Ｂから図Ｃのように残りの７分の２を持ち上げたとき、水面はさらに０.２４×２＝０.４８㎝下がります。
ここまでの流れをまとめてみると・・・
① 柱を３.２㎝持ち上げた→水面は０.８㎝下がった
② 柱をアの７分の５だけ持ち上げた→水面はさらに１.２㎝下がった
③ 柱をアの７分の２だけ持ち上げた→水面はさらに０.４８㎝下がった
つまり、柱が容器の底に触れている状態から水中を脱出する状態まで持ち上げることにより、次の図の緑色２か所の水がオレンジ色の部分に流れこみ、水面は０.８＋１.２＋０.４８＝２.４８㎝下がることが分かります。
このとき、次の図の緑色２か所を合わせた体積とオレンジ色の体積は等しいので、どちらも「底面積×高さ」の答えは等しくなります。
また、底面積の比は緑色２か所：オレンジ色＝４：１なので、高さの比はその逆比である１：４になります。
つまりオレンジ色の部分の高さは緑色の高さの４倍である２.４８×４＝９.９２㎝になるのですが、容器の高さは緑色とオレンジ色の高さの合計と等しいので、２.４８＋９.９２＝１２.４㎝になります。
PR
