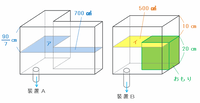
目盛りが付いた一辺４０㎝の立方体の水そうがあります。次の図１のように、水そうには一辺３０㎝の正方形の仕切りが底面に垂直に２枚付いていて、仕切りの内側には立方体の形をしたおもりがおいてあります。また、水そうの底面のうち、仕切りの内側にある部分は一辺３０㎝の正方形です。仕切りどうし、また仕切りと水そうの底面や側面はぴったり張り合わされています。水そうの底面の仕切りで分けられた各部分に、装置Ａ、Ｂが付いています。装置Ａは給水か排水をそれぞれ一定の割合で行います。また、装置Ｂは排水を一定の割合で行います。
※ 画像はすべて、クリックすると拡大します。
水の入っていない状態から、装置Ａだけを動かして給水し、水そうを水で満たしました。次の図２は給水し始めてからの時間と目盛りで調べた水面の高さの関係をグラフにしたものです。なお、水そうは水平においてあり、仕切りの厚さは考えません。このとき、次の問いに答えなさい。
(１)
毎秒何㎤の割合で給水しますか。
(２)
おもりの一辺の長さを求めなさい。
(３)
水そうが完全に水で満たされた状態で、同時に２つの装置Ａ、Ｂを動かして、それぞれ一定の割合で排水し始めました。次の図３は、排水し始めてからの時間と、目盛りで調べた水面の高さの関係をグラフにしたものです。排水し始めてから１６０秒より後で、仕切りで分けられた２つの水面の高さが同じになるのは、排水し始めてから何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
図２のグラフから、装置Ａを使って給水すると、２１０秒後には次の図のアの部分(真上から見るとＬ字型)に深さ３０㎝まで水が入ることが分かります。
※ 画像はすべて、クリックすると拡大します。
上の図の水そう全体の底面積は４０×４０＝１６００㎠、まだ水が入っていないイの部分の底面積は３０×３０＝９００㎠なので、アの部分の底面積は１６００－９００＝７００㎠です。
その部分に深さ３０㎝まで水が入ったので、装置Ａから２１０秒間給水すると、７００×３０＝２１０００㎤の水が入ることが分かります。
したがって、装置Ａからは１秒間に２１０００÷２１０＝１００㎤の水が入りました。
(２)
もし次の図のように、水そうからおもりを取り除いて給水すると、水そう全体を満たすのに必要な水の量は４０×４０×４０＝６４０００㎤になります。
しかし実際には、次の図のようにおもりが入っている分だけ水の量は少なくてＯＫなので、水そう全体を満たすのに必要な水の量は１００×５６０＝５６０００㎤ですみました。
※ 図２のグラフとさっきの問題の答えから、毎秒１００㎤ずつ５６０秒間給水したときに満水となることが分かります。
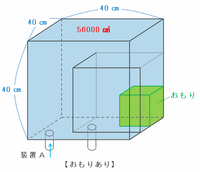
つまり、上の図のおもりの体積は６４０００－５６０００＝８０００㎤であることが分かるので、おもりの一辺の長さを□㎝とおくと、□×□×□＝８０００㎤と表せます。
８０００＝２０×２０×２０なので、おもりの一辺の長さは２０㎝になります。
(３)
図３のグラフから、最初の１６０秒間で水そうの深さが４０－３０＝１０㎝減ったことが読み取れます。
次の図のように、水そうの深さ１０㎝分の容積は４０×４０×１０＝１６０００㎤なので、装置ＡとＢから１秒間に排出される水の量は、合わせて１６０００÷１６０＝１００㎤です。
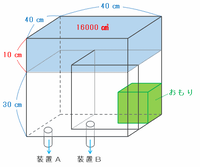
また、図３のグラフから、５８０－１６０＝４２０秒間で水そうのＬ字型の部分の水深が３０㎝減ったことも読み取れます。
次の図のＬ字型の部分の底面積は７００㎠なので、深さ３０㎝分の水の量は７００×３０＝２１０００㎤です。
その水はすべて装置Ａから排出されるので、装置Ａから１秒間に排出される水の量は２１０００÷４２０＝５０㎤になります。
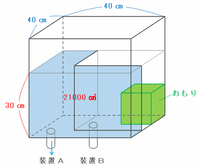
２つの装置から１秒間に排出される水の量は合わせて１００㎤、そして装置Ａから１秒間に排出される水の量は５０㎤なので、装置Ｂから１秒間に排出される水の量も、Ａと同じく１００－５０＝５０㎤になります。
水面の高さが３０㎝まで下がった後は、次の図のアの部分の水は装置Ａから、イの部分の水は装置Ｂから排出されます。
装置ＡとＢからはどちらも毎秒５０㎤の水が排出されますが、最初のうちはアの底面積がイよりも狭いので、水深の減り方はアの方が早いです。
ただし、イの水面がおもりの上端まで到着すると、そこからはイの方がアよりも底面積が狭くなって水深の減り方が早くなるので、再びアとイの水面の高さがそろいます。
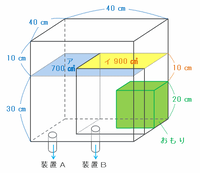
次の図のイの黄色い部分(おもりよりも上)にある水の容積は、３０×３０×１０＝９０００㎤です。
装置Ｂからは毎秒５０㎤ずつ排水されるので、９０００㎤の水が排水されるのにかかる時間は９０００÷５０＝１８０秒です。
装置ＡとＢはどちらも毎秒５０㎤ずつ排水するので、上の図で装置Ａから１８０秒間に排水される量も９０００㎤です。
ただし、アの底面積は７００㎠なので、９０００㎤排水されると水面が９０００÷７００＝７分の９０㎝下がります。
つまり、イの水面が１０㎝下がる時間でアの水面は７分の９０㎝下がるので、上の図のアとイの水面の高さの差は、７分の９０－１０＝７分の２０㎝になっています。
次の図のように、イの水面がおもりの上端まで到達すると、そこからはイの底面積が９００－２０×２０＝５００㎠に減ります。
一方、アの底面積はさっきまでと変わらず７００㎠のままなので、１秒間に５０㎤ずつ排水されたときの水面は、
・ア→１秒間に５０÷７００＝１４分の１㎝ずつ下がる
・イ→１秒間に５０÷５００＝１０分の１㎝ずつ下がる
ことから、水面の高さの差は１秒間に１０分の１－１４分の１＝３５分の１㎝ずつ縮まっていきます。
上の図の時点で、アとイの水面の高さは７分の２０㎝なので、その差が等しくなるまでにかかる時間は、７分の２０÷３５分の１＝１００秒です。
つまり、最初は水面の高さが４０㎝だった状態から、
・水面の高さが３０㎝になるまでにかかる時間→１６０秒
・アとイから９０００㎤ずつ排水されるのにかかる時間→１８０秒
・７分の２０㎝の差が等しくなるまでにかかる時間→１００秒
となることが分かるので、答えは１６０＋１８０＋１００＝４４０秒後になります。
【感想というか泣き言】
この問題、解くだけなら短時間でサクッとできるけど、解説用の作図が鬼のように面倒で心が半分折れました(笑)
PR
