容器Ａには１５％の濃さの食塩水１００ｇが、容器Ｂには３％の濃さの食塩水２００ｇが入っています。このとき、次の問いに答えなさい。
(１)
容器Ａから１０ｇ、容器Ｂから１０ｇの食塩水を同時に取り出しました。その後、容器Ａから取り出した１０ｇの食塩水を容器Ｂの中に、容器Ｂから取り出した１０ｇの食塩水を容器Ａの中に入れました。このとき容器Ｂの食塩水にふくまれる食塩の量は何ｇですか。
(２)
次に容器Ａの食塩水に水を１００ｇ加えました。容器Ａの食塩水の濃さは何％になりましたか。
(３)
次に容器Ａの食塩水にふくまれる食塩の量が容器Ｂの食塩水にふくまれる食塩の量の２倍になるようにしたいと思います。どちらの容器からどちらの容器に食塩水を何ｇ移したらよいですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
２つの容器の間で食塩水を１０ｇずつやり取りするとき、容器Ｂの中では次の図のように、
・容器Ａから来た濃さ１５％の食塩水１０ｇ
・容器Ｂに残った濃さ３％の食塩水１９０ｇ
の２つが混ざります。
※ 画像はすべて、クリックすると拡大します。
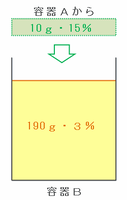
濃さ１５％の食塩水１０ｇに含まれる食塩の量は１０×０.１５＝１.５ｇ、濃さ３％の食塩水１９０ｇに含まれる食塩の量は１９０×０.０３＝５.７ｇなので、やり取りを終えた後の容器Ｂの中には食塩が１.５＋５.７＝７.２ｇ含まれています。
※ 容器ＡとＢとの間で食塩水を１０ｇずつ移し合っただけなので、容器Ｂに含まれる食塩水全体の量は、やり取りを終えた後も２００ｇのままです。
(２)
容器Ｂから食塩水が１０ｇやってくるとき、容器Ａの中では次の図のように、
・容器Ｂから来た濃さ３％の食塩水１０ｇ
・容器Ａに残った濃さ１５％の食塩水９０ｇ
・新たに追加した水１００ｇ
の３種類が混ざりあいます。
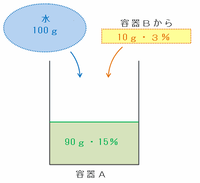
濃さ１５％の食塩水９０ｇに含まれる食塩の量は９０×０.１５＝１３.５ｇ、濃さ３％の食塩水１０ｇに含まれる食塩の量は１０×０.０３＝０.３ｇなので、やり取りを終えた後の容器Ａの中には食塩が１３.５＋０.３＝１３.８ｇ含まれています。
また、食塩水全体の量は９０＋１０＋１００＝２００ｇになるので、やり取りを終えた後の容器Ａに入っている食塩水の濃度は、１３.８÷２００×１００＝６.９％になります。
(３)
やり取りを終えた後の容器Ａに含まれる食塩の量は１３.８ｇ、容器Ｂに含まれる食塩の量は７.２ｇなので、２つの容器に含まれる食塩の量の合計は、次の図のように１３.８＋７.２＝２１ｇになります。
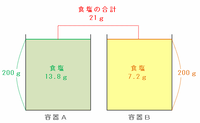
その２１ｇの食塩をＡ：Ｂ＝２：１の割合で比例配分すれば、容器Ａに含まれる食塩の量がＢの２倍になるので、
・容器Ａに含まれる食塩の量→２１×３分の２＝１４ｇ
・容器Ｂに含まれる食塩の量→２１×３分の１＝７ｇ
となることが分かります。
つまり、上の図だと容器Ｂは食塩の量が７.２－７＝０.２ｇ多いので、容器ＢからＡへ食塩水を何ｇか移してやればＯＫです。
容器Ｂの食塩水２００ｇには食塩が７.２ｇ含まれているので、食塩が０.２ｇ含まれるときの食塩水の量を□ｇとおくと、２００ｇ：７.２ｇ＝□ｇ：０.２ｇという比例式ができます。
□には２００×０.２÷７.２＝９分の５０ｇがあてはまるので、容器ＢからＡへ食塩水を９分の５０ｇ移せばＯＫです。
PR
