気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
05/04
Tue
2010
フェリス女学院2010【1】の(3) ☆公倍数・公約数☆
2つの整数A、Bについて、次の(あ)、(い)のことが分かっています。
(あ) A×B=7098
(い) B-A=143
① 整数A、Bの最大公約数を求めなさい。
② 整数Aを求めなさい。
※ 解説を見る場合は、下の「解説はこちらから」をクリック!
(1)
2つの整数A、Bの最大公約数を求めるには、普通は次の図のような連除法が使われます。
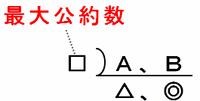
上の図から、7098は2×3×7×13×13と表せることが分かるのですが、その式の中で「13」だけが2回登場しているので、AとBの最大公約数は13になります。
上の図を利用してAとBをかけ算の式でそれぞれ表すと、A=△×□、B=◎×□となります。このとき、最大公約数である□はAとBどちらの式にも使われています。
次に、A×Bの答えである7098を素数のかけ算の式で表すため、素因数分解を行います。「素因数分解」って聞くとなんだか難しそうだけど、次の図のようにひとつの数で孤独に逆向きの割り算をやるだけのことです。
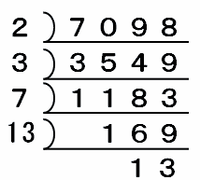
上の図から、7098は2×3×7×13×13と表せることが分かるのですが、その式の中で「13」だけが2回登場しているので、AとBの最大公約数は13になります。
(2)
A=△×□、B=◎×□のそれぞれの□に最大公約数である13をあてはめると、A=△×13、B=◎×13となります。
ちなみにこの△とか◎には、さっきの問題に出てきた7098=2×3×7×13×13のうち、「2・3・7」のどれかがあてはまります。
※ 例えば△→2×3、◎→7みたいな感じ。
このとき、B-A=◎×13-△×13=143と表せるのですが、式の中に「×13」が2回出てくるのでまとめると、(◎-△)×13=143となります。
つまり「◎-△」の答えは143÷13=11になるのですが、◎や△に「2・3・7」をあてはめて差を11にするには、◎→2×7、△→3のとき以外ありえません。
以上から、Aは3×13=39になります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
