サイコロは向かいあう面の目の和が７になっています。
サイコロを図１のように見ると、３つの面を同時に見ることができます。このときの見えている３つの目の数の和を『三面和』ということにします。図１の状態の三面和は６です。
平面上に置いたサイコロを、底面のひとつの辺を軸に回転させて倒したときの三面和を考えます。図２のように、図１の状態から右に１回倒したときの三面和は７です。また、図３のように図１の状態から手前に１回倒したときの三面和は９です。
次の問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１)
サイコロを右に続けて倒していきます。
図１の状態から２回倒したとき、図１の状態から３回倒したとき、図１の状態から４回倒したときの三面和をそれぞれ答えなさい。
(２)
サイコロを、まず右に１回倒し、次に手前に１回倒し、次に右に１回倒し、次に手前に１回倒し、次に右に１回倒し、・・・というように倒していきます。
(ア)
図１の状態から２回倒したとき、図１の状態から３回倒したとき、図１の状態から４回倒したときの三面和をそれぞれ答えなさい。
(イ)
図１の状態から、２０１０回倒したときまでの２０１１個の三面和の合計はいくつですか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
次の図のようにサイコロを右に１回倒すと、正面の目はそのまま残り、真上の目は右側に移動し、右側の目は底面になって見えなくなり、その代わりに左側の目が真上に移動します。
その決まりに従って右へどんどん倒していくと、次のような図になります。
上の図から、２回倒したときの三面和は２＋４＋６＝１２、３回倒したときの三面和は２＋３＋６＝１１、そして４回倒したときの三面和は最初の図と同じく１＋２＋３＝６になります。
(２)の(ア)
次の図のようにサイコロを手前に１回倒すと、真上の目は正面に移動し、右側の目はそのまま残り、正面の目は底面になって見えなくなり、その代わりに後ろ側の目が真上に移動します。
図１の状態から「右→手前→右→手前」の順にサイコロを倒し、再び図１の状態に戻るまでの図を完成させてみると次のようになります。
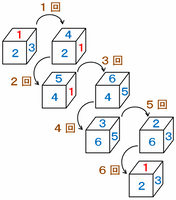
上の図から、２回倒したときの三面和は１＋４＋５＝１０、３回倒したときの三面和は４＋５＋６＝１５、そして４回倒したときの三面和は３＋５＋６＝１４になります。
(２)の(イ)
さっきの図を見れば分かるように、スタートから６回倒すと最初と同じ三面和のサイコロに戻ります。また、三面和は１回倒すごとに「７→１０→１５→１４→１１→６」と変化しており、その組み合わせが２０１０回の中に２０１０÷６＝３３５組あります。
倒した回数１回目から２０１０回目までの三面和の合計は、(７＋１０＋１５＋１４＋１１＋６)×３３５＝２１１０５です。
ただ、この問題はスタートのときの三面和である６もふくめた２０１１個の三面和の合計を求めなければいけないので、答えは６＋２１１０５＝２１１１１になります。
PR
