北アメリカ大陸には、何年かごとにあるせまい地域に集中して大量発生する特別な種類のセミがいます。たとえば、２００４年にある地域で５０億匹のセミが大量発生したときは、１７年ごとに大量発生するセミだったので、１７年ゼミと呼ばれました。このようなセミの大量発生について、次の各問いに答えなさい。
(１)
５０億匹のセミが、およそ１.２５㎢の範囲に集中して発生したとします。このとき、もし家の庭が６ｍ×４ｍの長方形と同じ広さだとしたら、この家の庭には、何匹のセミが発生することになりますか。ただし、セミは範囲内に均等に発生するものとします。
(２)
１２年ゼミ、１８年ゼミ、１３年ゼミ、１７年ゼミがある年に同時に大量発生したとします。この次に、１３年ゼミと１７年ゼミが大量に発生するのは、１２年ゼミと１８年ゼミがこの次に大量に発生する年の何年後になりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
１.２５㎢に５０億匹のセミがいるので、１㎢あたりのセミの数は、次の図のように５０億÷１.２５＝４０億匹になります。
※ 画像はすべて、クリックすると拡大します。
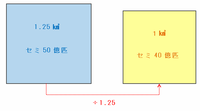
また、１㎢は次の図のように１辺の長さが１㎞＝１０００ｍの正方形の土地なので、１㎢と１㎡は１０００×１０００＝１００万倍の関係です。
つまり、１㎢に４０億匹のセミがいるのなら、１㎡あたりのセミの数は４０億÷１００万＝４０００匹であることが分かります。
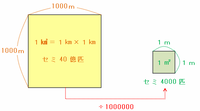
庭の面積は６×４＝２４㎡なので、その庭にいるセミの数は４０００×２４＝９６０００匹になります。
【補足】
１.２５㎢×１０００×１０００＝１２５００００㎡なので、１２５００００㎡：２４㎡＝５０億匹：□匹という比例式を解けば庭にいるセミの数が求められます。
つまり、別に１㎢あたりのセミの数なんて求めなくてもＯＫなのですが、個人的には「１単位あたりの数量に着目するのは算数の基本じゃないの？」と思ってるので、その方法で解説を作ってみました。
たぶん「１２５００００÷２４」の計算にトライした受験生は少数派だと思う(いかにも割り切れなさそう)けど、それでも分数を使えばちゃんと答えにたどり着けるので、自分の計算力や好みに合わせて解いてください。
(２)
１３年ゼミと１７年ゼミが次に大量に発生するのは、１３と１７の最小公倍数である２２１年後です。
また、１２年ゼミと１８年ゼミが次に大量に発生するのは、１２と１８の最小公倍数である３６年後です。
したがって、答えは２２１－３６＝１８５年後になります。
PR
