１、２、３、４、５の５つの数を並べて、隣り合う数を足し合わせる操作を４回します。たとえば、５つの数を「１・３・５・２・４」と並べたとき、次の図のようになります。
※ 画像はすべて、クリックすると拡大します。
(１)
上のような操作をしたとき、次の図のようになりました。ア、イにあてはまる数をそれぞれ答えなさい。
(２)
上のような操作をしたとき、次の図のようになりました。このとき、
① ◎にあてはまる数を答えなさい。
② Ａ、Ｂ、Ｃ、Ｄの４つの数の和と、☆にあてはまる数を答えなさい。
③ Ａ、Ｂ、Ｃ、Ｄにあてはまる数をそれぞれ答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
たとえば次の図の２＋Ａの答えが３になるので、Ａには３－２＝１があてはまります。また、３＋Ｄの答えが９なので、Ｄは９－３＝６になります。
さらに、Ｄ＝６、Ａ＝１であることが分かったので、Ｂには６－１＝５があてはまります。
そうやって分からないマスを少しずつ埋めていけば、アとイの数にそのうちたどり着けるはずです。
※ 画像はすべて、クリックすると拡大します。
次の図の９＋Ｇの答えが２３なのでＧは２３－９＝１４、そして６＋Ｅの答えがＧ(つまり１４)なので、Ｅは１４－６＝８になります。
つまり、下の図の５＋アの答えが８になるので、アには８－５＝３があてはまります。
また、最上段には左から順に「２・１・５・３」と並んでいることも分かったので、右端のＣには１から５の中でまだ使われていない４があてはまります。
最上段の５つの数の並び方は次の図のようになることが分かったので、あとはイに向けて普通に足し算をしていけばＯＫです。
下の図のＦは３＋４＝７、Ｈは８＋Ｆ＝８＋７＝１５、Ｉは１４＋Ｈ＝１４＋１５＝２９なので、イには２３＋２９＝５２があてはまります。
(２)の①
次の図のアには１２と◎の合計があてはまるので、アは「１２＋◎」と表せます。また、イには◎と１１の合計があてはまるので、そちらは「◎＋１１」となります。
下の図のアとイの合計が４７になるので、(１２＋◎)＋(◎＋１１)＝４７と表せます。
(１２＋◎)＋(◎＋１１)＝２３＋◎＋◎＝４７なので、◎２つ分の合計は４７－２３＝２４です。
したがって、◎には２４÷２＝１２があてはまります。
(２)の②
次の図のアはＡ＋Ｂ、イはＢ＋☆、ウは☆＋Ｃ、エはＣ＋Ｄがそれぞれあてはまるので、下段の左端にある「１２」はア＋イ＝Ａ＋Ｂ＋Ｂ＋☆、真ん中の「１２」はイ＋ウ＝Ｂ＋☆＋☆＋Ｃ、そして右端の「１１」はウ＋エ＝☆＋Ｃ＋Ｃ＋Ｄの答えをそれぞれ表しています。
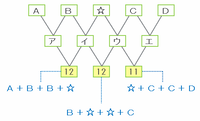
その３つの式を次の図のように並べてみると、式①と②は合計がどちらも１２で、しかも左辺にはどちらも「Ｂ＋☆」があるので、式①の「Ａ＋Ｂ」と式②の「☆＋Ｃ」の答えは等しいことが分かります。
つまり、上の図の式③の「☆＋Ｃ」の部分を「Ａ＋Ｂ」と入れ替えてもＯＫなので、式③は☆＋Ｃ＋Ｃ＋Ｄ＝Ａ＋Ｂ＋Ｃ＋Ｄ＝１１と変形できます。
したがって、Ａ、Ｂ、Ｃ、Ｄの４つの数の和は１１になります。
また、Ａ、Ｂ、Ｃ、Ｄと☆の５つのマスには１から５のどれかが入り、その５つの数の合計は１＋２＋３＋４＋５＝１５なので、☆には１５－１１＝４があてはまります。
(２)の③
さっきの問題で☆＝４であることが分かったので、Ａ～Ｄのマスには「１・２・３・５」のどれかがあてはまります。
次の図のように、式①～③の☆にそれぞれ４をあてはめてみると、
・式①→Ａ＋Ｂ＋Ｂ＋☆＝Ａ＋Ｂ＋Ｂ＋４＝１２
・式②→Ｂ＋☆＋☆＋Ｃ＝Ｂ＋４＋４＋Ｃ＝１２
・式③→☆＋Ｃ＋Ｃ＋Ｄ＝４＋Ｃ＋Ｃ＋Ｄ＝１１
となります。
上の図の式①はＡ＋Ｂ＋Ｂ＋４＝１２となったので、Ａ＋Ｂ＋Ｂの部分は１２－４＝８になります。
「１・２・３・５」の中から２つの数を選んでＡ＋Ｂ＋Ｂ＝８となるのは「２＋３＋３」のときしかないので、Ａは２、Ｂは３であることが分かります。
また、式③は４＋Ｃ＋Ｃ＋Ｄ＝１１となったので、Ｃ＋Ｃ＋Ｄの部分は１１－４＝７になります。
「１・２・３・５」の中でさっき使わなかった１をＣに、５をＤにあてはめるとちょうど１＋１＋５＝７となるので、Ｃは１、Ｄは５になります。
PR
