気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
02/07
Mon
2011
慶応中等部2011【1】の(4) ☆分数・分子や分母に数を加える問題☆
ある分数があります。その分子に4を加えたら2分の1になりました。また、もとの分数の分子と分母にそれぞれ3を加えたら5分の2になりました。もとの分数はいくつですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
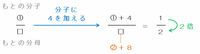
もとの分数の分子を①、分母を□とおくと、4を加えたときの分子は「①+4」と表せます。
次の図のように、そのときの分数の大きさが2分の1になるので、もとの分母である□は「①+4」の2倍にあたる「②+8」と表せます。
※ 画像はすべて、クリックすると拡大します。
次の図のように、もとの分子を①、もとの分母を②+8として、それぞれに3を加えてみると、分子は①+3、分母は②+11と表せます。
次の図のように、もとの分子を①、もとの分母を②+8として、それぞれに3を加えてみると、分子は①+3、分母は②+11と表せます。
また、そのときの分数の大きさが5分の2となることから、分子である「①+3」と分母である「②+11」の比は2:5であることも分かります。

そこで、分子「①+3」を5倍、分母「②+11」を2倍して大きさをそろえてみると、
そこで、分子「①+3」を5倍、分母「②+11」を2倍して大きさをそろえてみると、
・分子→(①+3)×5=⑤+15
・分母→(②+11)×2=④+22
となります。
その2つの数を次のように2本の線分図に直して比べてみると、比の⑤-④=①が22-15=7にあたることが分かります。

つまり、もとの分数の分子は7、そして分母は7×②+8=22なので、もとの分数は22分の7になります。
************ いいわけコーナー *******************************
5分の2となるときの分子は①+3、分母は②+11なので、分子を5÷2=2.5倍すれば大きさがそろいます。
(①+3)×2.5=2.5+7.5なので、比の2.5-2=0.5が11-7.5=3.5となり、比の1は3.5÷0.5=7になります。
・・・という流れで解説を作ろうかなー、と思っていたのですが、このブログだと比の2.5とか0.5を丸囲みの数字で表すことができないので、比が小数にならない方法を採用しました。
************ おしまい *******************************
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
