気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
03/30
Tue
2010
開成2010【1】の(3) ☆分数☆
例えば「5=△+□」の△や□にあてはまる数は、足し算の答えである5よりも小さい数があてはまりますね。
というわけで、この問題の△には12よりも大きい数(小さい数ではない!なぜなら、△は分数の分母だから。分母に小さい数ををあてはめたら、分数自体は大きい数になってしまう)があてはまります。
また、12分の1を半分にすると24分の1になるので、△には24以下の数があてはまります。
※ △が24よりも大きくなる→□は24よりも小さくなる→問題文の条件に合わないので×
というわけで、さっそく△に13から24までの数をあてはめて、サクサクと□を求めていきましょう。
※ 画像はすべて、クリックすると拡大します。
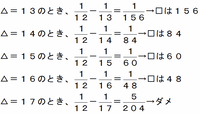

以上から、△と□にあてはまる組み合わせは、
※ 画像はすべて、クリックすると拡大します。
はい、くじけずに最後までがんばりましょう(笑)
以上から、△と□にあてはまる組み合わせは、
(13・156)、(14・84)、(15・60)、(16・48)、(18・36)、(20・30)、(21・28)、(24・24)
の計8組あることが分かります。
※ 17・19・23は素数なので、計算するまでもなく分子が1にはならない(約分できない)ですね。ただし、13は12のすぐとなりなので、約分できなくても分子は13-12=1になります。また、12は2または3で割り切れる整数なので、2や3の倍数との組み合わせなら約分でき、結果として分子が1になる可能性が高いと予想できます。
※ 例えば△=22のとき、12=2×2×3、22=2×11、22-12=10=2×5なので、分子の10を約分して1にするために必要な「5」が、「12」と「22」の中にないことが分かります。まぁ、そんなこんなでいちいち通分して引き算する必要はないのですが、もしそれが思いつかなかったとしても、地道に計算すればちゃんと解けるのでOKです。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
