気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
03/30
Tue
2010
関東学院2009【7】 ☆比☆
ある工場では部品Aが5個と部品Bが3個とで製品が1個できます。最初に部品Aと部品Bの個数の比は9:5でした。どちらかの部品がなくなるまで製品を作ったら、どちらかの部品だけが56個余りました。製品は何個できましたか。
※ 解説を見るには、右下の「解説はこちらから」をクリック!
製品を作るために使う部品の個数の比は、A:B=5:3と表せます。
最初にある部品の個数の比はA:B=9:5なので、まずはこの2つの比のBをそろえて(別にAでもかまいません)、2つの比をならべてみます。
※ 画像はクリックすると拡大します。
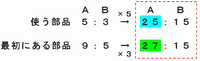
上の赤いわくの中を見比べてみれば分かるように、最初にある部品B(比の15)をすべて使ったとき、部品Aはまだ27-25=2残っています。
※ 画像はクリックすると拡大します。
上の赤いわくの中を見比べてみれば分かるように、最初にある部品B(比の15)をすべて使ったとき、部品Aはまだ27-25=2残っています。
この比の2が部品の余りである56個にあたるので、比の1は56÷2=28個だと分かります。
製品を作るのに使った部品Bの数は、28×15=420個です。
製品1個を作るのに部品Bを3個ずつ使うので、完成する製品の数は、420÷3=140個になります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
