気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
04/11
Sun
2010
女子学院2010【8】 ☆割合・相当算☆
ある品物の仕入れ値に、300円の利益を見込んで定価をつけた。Aさんは定価の10%引きで15個売り、Bさんは定価の20%引きで20個売ったところ、AさんとBさんの利益の比は9:4になった。
(1)
定価の10%引きで売ったときと、定価の20%引きで売ったときの1個あたりの利益の比を、最も簡単な整数比で表すと( ):( )である。
(2)
この品物の仕入れ値は( )円である。
※ 解説を見たい場合は、下の「解説はこちらから」をクリック!
(1)
定価の10%引きで15個売ったときの利益を【9】とおくと、1個あたりの利益は【9】÷15=【0.6】と表せます。
また、定価の20%引きで20個売ったときの利益を【4】とおくと、1個あたりの利益は【4】÷20=【0.2】と表せます。
つまり、それぞれの1個あたりの利益の比は、0.6:0.2=3:1となります。
※ この答えはもちろん、次の問題を解くための手掛かりになります。
(2)
この商品の仕入れ値を[1]とおくと、定価は[1]+300円と表せます。
・定価の10%引き→([1]+300円)×0.9=[0.9]+270円
・定価の20%引き→([1]+300円)×0.8=[0.8]+240円
この2つの式を、次のような線分図に表してみます。
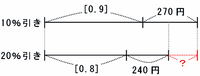
(画像はすべて、クリックすると拡大します)
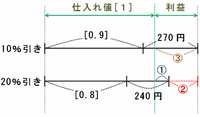
利益とは「仕入れ値よりも余分な金額の部分」のことなので、上の図の緑色の点線よりも右側がそれぞれの利益になります。
このとき、上の図の赤い?の部分である[1.05]-[0.8]=[0.25]が、240-15=225円にあたります。
(画像はすべて、クリックすると拡大します)
上の図の赤い?の部分(2つの売り値の差)は、[0.9]-[0.8]=[0.1]、270-240=30円なので、[0.1]+30円と表せます。
そして今度は次のように、仕入れ値やそれぞれの利益の割合(さっきの問題で求めた③とか①のこと)もふくめて線分図に書き込んでみます。
利益とは「仕入れ値よりも余分な金額の部分」のことなので、上の図の緑色の点線よりも右側がそれぞれの利益になります。
また、上の線分図の利益が③、下の線分図の利益が①なので、その差である赤い部分は③-①=②と表せます。
つまり②=[0.1]+30円なので、①はその半分である[0.05]+15円だと分かります。
このとき、上の線分図の[0.8]+240円の長さは、緑色の仕入れ値[1]と青色の①を合わせた長さと同じになっています。
青色の①は[0.05]+15円のことなので、仕入れ値[1]と合わせると[1.05]+15円と表せます。
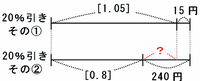
つまり、定価の20%引きのときの売り値は、次の図のように[0.8]+240円あるいは[1.05]+15円という2つの表し方があるのです。
このとき、上の図の赤い?の部分である[1.05]-[0.8]=[0.25]が、240-15=225円にあたります。
つまり、仕入れ値の[0.25]が225円にあたることが分かったので、この商品の仕入れ値は、225÷[0.25]=900円になります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
