Ａ、Ｂ、Ｃ、Ｄの４人がはじめいくらかずつのお金を持っていて、ＢはＣよりも２５０円多く持っていました。まず、Ａは所持金の７分の１をＤに、Ｂは所持金の１９分の１をＣにあげました。次に、ＡはＣに、ＢはＤにそれぞれ残りの所持金の６分の１をあげました。さらに、ＡはＢに、残りの所持金の５分の１をあげたところ、４人の所持金はすべて同じになりました。このとき、次の問いに答えなさい。
(１) ＡとＢの初めの所持金の比を、もっとも簡単な整数の比で表しなさい。
(２) Ａの初めの所持金は何円ですか。
(３) Ｄの初めの所持金は何円ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、４人の最初の所持金をそれぞれ１とおいて、３段階のやり取りの後の所持金の割合をそれぞれ確認してみます。
※ 画像はすべて、クリックすると拡大します。
【やり取り その１】
最初のやり取りでは、Ａが所持金の７分の１をＤに、Ｂが所持金の１９分の１をＣにあげたので、次の図のようにＣとＤは所持金が増え、ＡとＢは所持金が減ります。
また、Ａの所持金は１－７分の１＝７分の６、そしてＢの所持金は１－１９分の１＝１９分の１８になります。
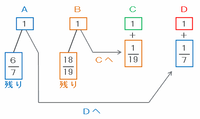
【やり取り その２】
２回目のやり取りでは、ＡはＣに、ＢはＤにそれぞれ残りの所持金の６分の１をあげたので、次の図のようにＣとＤの所持金はさらに増えます。
このとき、ＡからＣへ渡った所持金の割合は７分の６×６分の１＝７分の１なので、Ａの残金は７分の６－７分の１＝７分の５に減りました。
また、ＢからＤへ渡った所持金の割合は１９分の１８×６分の１＝１９分の３なので、Ｂの残金は１９分の１８－１９分の３＝１９分の１５になりました。
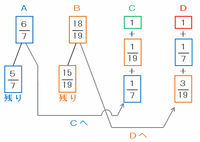
【やり取り その３】
３回目のやり取りでは、次の図のようにＡの残金の５分の１がＢへ渡ったため、Ａの所持金は減りＢの所持金は増えました。
このとき、ＡからＢへ渡された所持金の割合は７分の５×５分の１＝７分の１なので、Ａの残金の割合は７分の５－７分の１＝７分の４になります。
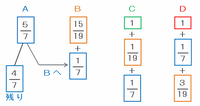
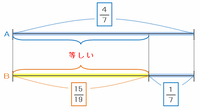
上の図の４人の残金が等しくなったので、ＡとＢの残金の割合を２本の線分図に表して次のように比べてみると、Ａの所持金の７分の４－７分の１＝７分の３と、Ｂの所持金の１９分の１５が等しいことが分かります。
つまり、Ａ×７分の３とＢ×１９分の１５が等しいことから、Ａ：Ｂ＝３分の７：１５分の１９＝３５：１９になります。
(２)
Ａの最初の所持金を比の３５、Ｂの最初の所持金を１９とおくと、やり取りをすべて終えた後の４人の所持金はそれぞれＡの７分の４にあたるので、３５×７分の４＝２０と表せます。
やり取りをすべて終えた後のＣの所持金は、「Ｃがもともと持っていた１」と「Ｂの１９分の１」と「Ａの７分の１」の３種類が混ざっています。
その合計が比の２０と表せるので、次の図のＢに１９を、そしてＡには３５をあてはめてみると、Ｃの最初の所持金である「Ｃ×１」の部分は２０－(１＋５)＝１４と表せることが分かります。
Ｂの最初の所持金の比は１９、そしてＣの最初の所持金の比は１４なので、その差である比の１９－１４＝５が、ＢとＣの最初の所持金の差である２５０円にあたることが分かります。
比の１は２５０÷５＝５０円なので、の最初の所持金の比である３５は５０×３５＝１７５０円になります。
(３)
やり取りをすべて終えた後のＤの所持金は、「Ｄがもともと持っていた１」と「Ａの７分の１」と「Ｂの１９分の３」の３種類が混ざっています。
その合計が比の２０と表せるので、さっきと同じように次の図のＡに３５を、そしてＢには１９をあてはめてみると、Ｄの最初の所持金は２０－(５＋３)＝１２と表せます。
比の１は５０円なので、Ｄの最初の所持金は５０×１２＝６００円になります。
PR
