ある店では、１本３２円で何本かだんごを仕入れました。そのうちの何本かは売れ残ることを予想して、利益が５０００円になるように１本６０円で売りました。ところが、売れ残っただんごの本数が予想した数の４０％だったので、利益は５３６０円となりました。次の問いに答えなさい。(式または考え方を書きなさい)
(１) 売れ残ると予想しただんごの本数を求めなさい。
(２) 仕入れただんごの本数を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは「売れない」と予想した本数のだんごが１本売れるごとに、利益は何円ずつ増えていくのかを確認してみます。
【予定の図】
このだんごの仕入れ値は１本３２円なので、１本売るごとに６０－３２＝２８円ずつもうかります。
まずは次の図を使って、最初の予定をカンタンに説明してみると・・・
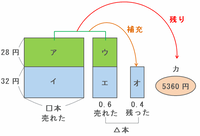
① 下の図の□本を売れば、とりあえず緑色の長方形アの分だけもうかる。
② でも、売れない△本の分の仕入れ値は回収できそうにないので、その金額は長方形アからウへ補充する。
③ それでもまだ５０００円残るはずなので、それが最終的な利益となる。
という流れになっています。
※ 画像はすべて、クリックすると拡大します。
【実際の図】
実際には次の図のように、売れ残っただんごの本数が予想の４０％＝０.４でした。
つまり売れ残る予定だっただんごの１－０.４＝０.６が売れた結果、
① 予定よりも多く売れたので、とりあえず長方形ウの分ももうかった。
② 長方形オの仕入れ値は回収できなかったので、その金額は長方形アとウから補充した。
③ でも予定よりも売れ残った本数が減ったので、補充すべき金額は少なくて済んだ。
④ ①と③のダブル効果で最終的な利益がアップして５３６０円になった。
という流れになりました。
このとき、予定では売れ残るはずだっただんごが１本売れるごとに、
① 回収できないはずだった仕入れ値の３２円を補充する必要がなくなる。
② おまけにだんごが売れて２８円もうかる。
ので、最終的な利益は１本につき３２＋２８＝６０円ずつ増えていきます。
最終的な利益は予定よりも５３６０－５０００＝３６０円増えたことから、予定よりも多く売れただんごの本数は３６０÷６０＝６本だと分かります。
つまり次の図のように、売れ残る予定だった△本のだんごの０.６が６本にあたるので、答えは６÷０.６＝１０本になります。
(２)
さっきの問題で「売れない」と予想しただんごの数は１０本であることが分かったので、ここからは面積図を利用して仕入れた本数を求めてみます。
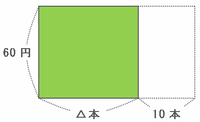
このお店は□本のだんごを１本３２円で仕入れたので、仕入れ値の合計は次のような青色の長方形で表すことができます。
※ ３２円×□本＝仕入れ値の合計
ただ、最初の予定では５０００円もうかることになっていたので、下の図のように利益の５０００円を付け足して予定の総売り上げの図にしてみます。
※ 仕入れ値の合計＋予定の利益の合計＝予定の総売り上げ
また、最初の予定では１０本売れ残ることになっていたので、そのときに売れた本数を△本とおくと、予定の総売り上げは次のような緑色の長方形に表すことができます。
※ 売り値×売れた本数＝総売り上げ
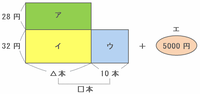
この２つの図を重ね合わせると、次のような面積図ができます。
このとき、下の図のア＋イの面積はイ＋ウ＋エの面積と等しいので、アの面積はウ＋エの面積と同じであることが分かります。
また、この問題で求めたいのは仕入れただんごの本数なので、最終的には下の図の□本にあてはまる数が答えになります。
上の図のウの長方形は３２×１０＝３２０円なので、ウとエの和は３２０＋５０００＝５３２０円です。
つまりアの長方形も５３２０円なので、上の図の△本(最初に売れると予想した本数)は５３２０÷２８＝１９０本になります。
仕入れた本数はそれよりも１０本多いので、答えは１９０＋１０＝２００本です。
PR
