次の図のように円を並べていきます。円の中の数字は、その円と接している円の個数を表しています。次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) ５段のとき、円の中の数字の和を求めなさい。
(２) 円の中に４と書かれた円が８７個あるとき、６と書かれた円は何個ありますか。
(３) 円の中に６と書かれた円が４９５０個あるのは、何段のときですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
実際に５段の図を使って規則性を確かめながら、円の中の数字の和を求めてみます。
次の図のように、５段積んでできた三角形の３つの頂点にある青い円は、どれも黄色い２個の円と接しているので「２」と書き込みます。
※ 画像はすべて、クリックすると拡大します。
今度は三角形の外周にある緑色の円に注目してみると、下の図のようにどちらも黄色い４個の円と接しているので、緑色の円の中に「４」と書きます。
最後に三角形の内側にある赤色の円を見てみると、
・上から３段目→赤い円が１個でき、その周りには黄色い円が６個ある。
・上から４段目→赤い円が２個でき、その周りには黄色い円が６個ある。
ことから、３つの赤色の円すべてに「６」と書き込みます。
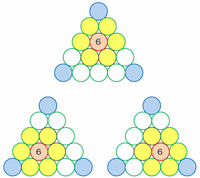
これまでの流れをふまえて５段のすべての円に数字を書き込むと次の図のようになります。
大切なポイントとしては、
・三角形の３つの頂点にある青色の円はすべて「２」となる。
・三角形の外周にある緑色の円はすべて「４」となる。
・三角形の上から３段目以降にできる内側の円はすべて「６」となる。
ということがあげられます。
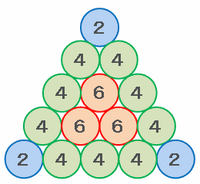
上の図には青色の円が３個、緑色の円が３×３＝９個、赤色の円が１＋２＝３個あるので、すべての数字の和は２×３＋４×９＋６×３＝６０になります。
(２)
「４」と書かれた８７個の円は、次の図のように三角形の外側にある３本の辺に８７÷３＝２９個ずつ並んでいます。
このとき下の図を見れば分かるように、この三角形全体は１＋２９＋１＝３１段になっています。
「６」と書かれた赤色の円は、次の図のように上から３段目で初めて１個登場し、その後は１段下がるにつれて１個ずつ増えていきます。
また、赤色の円は「てっぺんの２段」と「最底辺の１段」との間にできるので、下の図の赤い円は全部で３１－(２＋１)＝２８段に並びます。
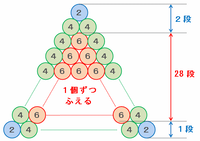
つまり「６」と書かれた赤い円は、赤いピラミッドの上から１段目には１個、２段目には２個、３段目には３個、・・・、２８段目には２８個といった感じで並んでいるので、赤い円の個数は１から２８までの和を計算すれば求められます。
以上から、答えは(１＋２８)×２８÷２＝４０６になります。
(３)
まずは「６」と書かれた赤い円を４９５０個積んだピラミッドに注目してみると、赤い円は最上段に１個、２段目に２個、３段目に３個・・・のように１個ずつ増えていき、最後の□段目には□個の赤い円が並んでいます。
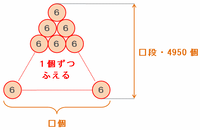
このとき、１から□までの整数の和が赤い円の個数である４９５０になるので、(１＋□)×□÷２＝４９５０という式ができます。
その式を逆算すると「(１＋□)×□」の答えが４９５０×２＝９９００となるのですが、「１＋□」は「□」よりも１大きい数なので、たとえば「６と５」や「９と８」のように連続する２つの整数の積が９９００になる場合を見つければ、□にあてはまる数が分かります。
というわけで、さっそく頭の中でモゾモゾ考えてみると、９９００＝１００×９９なので、□には９９があてはまります。
つまり赤い円のピラミッドは９９段あることが分かったのですが、青と緑の円もふくめたピラミッド全体には、次の図のように「てっぺんの２段」と「最底辺の１段」があるので、答えは２＋９９＋１＝１０２段になります。
PR
