ある中学校の全校生徒の人数の、７分の４は運動部に入部しており、３分の２はめがねをかけています。いま、運動部でめがねをかけている生徒は８０人います。このとき、次の問いに答えなさい。
(１)
考えられる全校生徒の人数が最も多いときの、運動部員の人数は何人ですか。
(２)
考えられる全校生徒の人数が最も少ないときの、めがねをかけている生徒は何人ですか。なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
(３)
全校生徒の人数は何通り考えられますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは問題文に出てくる２つの分数を、次のように通分しておきます。
・運動部に入部している生徒・・・全校生徒の７分の４→２１分の１２
・めがねをかけている生徒・・・全校生徒の３分の２→２１分の１４
問題文をベン図に表すとき、「運動部に入部している生徒」の円と「めがねをかけている生徒」の円との関係は、次の図のようにいろいろな状態が考えられます。
※ 画像はすべて、クリックすると拡大します。
全校生徒の数をなるべく多くするには、運動部でめがねをかけている８０人の割合が最も小さいときを考えればＯＫなので、上のベン図の中でも最も重なりの面積がせまいものを選びます。
また、次のベン図のアイが２１分の１２、イウが２１分の１４、エが０のとき、アイウが全校生徒の割合である１になります。
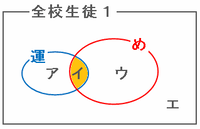
※ エが０→ウチの学校には、運動部にも入らずめがねもかけてない奴など１人もおらんわ！
このとき、２１分の１２＋２１分の１４－１＝２１分の５が、上の図のアイ＋イウ－アイウ＝イの割合になります。
つまり、全校生徒の２１分の５が８０人にあたるので、全校生徒の人数は８０÷２１分の５＝３３６人、そして運動部員の人数は３３６×２１分の１２＝１９２人になります。
(２)
全校生徒の人数をなるべく少なくするには、運動部でめがねをかけている８０人の割合が最も大きいときを考えればＯＫなので、次のように小さい円が大きい円の中にすっぽり入っているベン図を使って考えます。
※ 「ウチの学校では、運動部の奴らは全員めがねをかけとるんじゃ！」という図。
上の図のア(全校生徒の２１分の１２)が８０人なので、全校生徒の数は８０÷２１分の１２＝１４０人、そしてめがねをかけている生徒はその２１分の１４にあたるので、１４０×２１分の１４＝・・・
・・・あれ？答えが整数にならない。
よく考えてみれば、「□×２１分の１４」の答えを整数にしたければ、次の図のように□は２１の倍数じゃなきゃダメですよね。
このとき、１４０よりも大きい整数の中で最も小さい２１の倍数は２１×７＝１４７なので、それが問題文の条件にあてはまる全校生徒の数の中で最も小さい場合になります。
したがって、めがねをかけている生徒の数は１４７×２１分の１４＝９８人になり、そのときのベン図は次のように、小さい円が大きい円の中にすっぽりと入るちょっと手前の状態になっています。
(３)
これまでの２つの問題で分かったことをまとめてみると・・・
・全校生徒の数が最も少ない場合→(２)で求めた１４７人＝２１×７
・全校生徒の数が最も多い場合→(１)で求めた３３６人＝２１×１６
つまり、問題文の条件に合う全校生徒数は、「２１×□」の□に７から１６までの整数をあてはめた答えの数だけ考えられます。
７から１６までの整数は全部で１６－６＝１０個あるので、答えは１０通りになります。
PR
