図１は平らでなめらかな長方形の台を真上から見たものです。ＣやＥに球を置き、その球を辺ＡＤに向かって転がします。辺ＡＤと辺ＡＢには壁があり、壁に当たった球は、図２のようにアとイの角の大きさが等しくなるようにはね返ります。ただし、球の大きさと壁の厚みは考えないものとします。
※ 画像はクリックすると拡大します。
(１)
Ｃに球を置き、転がしたところ、壁に１回だけはね返ってＢにたどり着きました。壁にはね返ったときのアにあたる角の大きさは何度ですか。
(２)
Ｅに球を置き、転がします。
①
球が壁に１回だけはね返って、Ｂにたどり着きました。はね返ったところは、Ａから何ｍですか。
②
球が壁に２回はね返って、Ｃにたどり着きました。最初にはね返ったところは、Ａから何ｍですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
Ｃを出発した球が辺ＡＤではね返って一発でＢに着くためには、次の図のように辺ＡＤの真ん中にある点Ｆでパコーンと折り返せばＯＫです。
※ 画像はすべて、クリックすると拡大します。
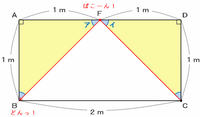
このとき、上の図の左右にできる三角形ＡＢＦと三角形ＤＣＦはどちらも直角二等辺三角形になっているので、角アの大きさは４５度になります。
(２)の①
Ｅを出発した球が辺ＡＤではね返って一発でＢに着くのは、次の図のように辺ＡＤの真ん中よりも右寄りにある点Ｆでカキーンと折り返したときです。
このとき、三角形ＡＢＦと三角形ＤＥＦの内角を比べてみると・・・
・角ＡＦＢと角ＤＦＥはどちらも球がはね返ったときにできるので同じ大きさ。
・角ＢＡＦと角ＥＤＦはどちらも直角。
・残りの角ＡＢＦと角ＤＥＦの大きさも自動的に等しいことになる。
というわけで、三角形ＡＢＦと三角形ＤＥＦは相似であることが分かります。
また、辺ＡＢと辺ＤＥの長さの比がＡＢ：ＤＥ＝２：１なので、辺ＡＦと辺ＦＤの長さの比も２：１になっているはずです。
辺ＡＦと辺ＡＤの長さの和は２ｍ、ＡＦ：ＡＤ＝２：１なので、辺ＡＦの長さは２ｍの３分の２にあたります(比例配分)。
以上から、はね返る地点はＡから２×３分の２＝３分の４ｍはなれたところです。
(２)の②
Ｅを出発した球が２回はね返ってＣに着く場面をイメージするのはちょっと難しいかもしれないけど、次の図のように点ＦとＧで「パコーン」「カキーン」と折り返したときなら条件にあてはまります。
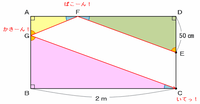
上の図の中には３つの相似な三角形がある(ＡＧＦとＤＥＦとＢＧＣ)のですが、それだけではＡＦの長さがうまく求められないので、三角形ＡＧＦとまったく同じものを１つ作り、それを次の図のように辺ＡＧの左側にくっつけてみます。
このとき、上の図の三角形ＨＣＤと三角形ＦＥＤは次のように相似になっており、辺ＤＣと辺ＤＥの長さの比がＤＣ：ＤＥ＝１ｍ：０.５ｍ＝２：１なので、辺ＨＤと辺ＦＤの長さの比も２：１になっているはずです。
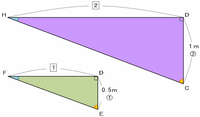
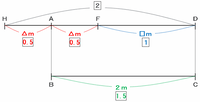
このとき、辺ＦＤの長さを□ｍ、辺ＡＦやＨＦの長さを△ｍとおき、長方形の底辺である辺ＢＣの長さと比べてみると、次のような線分図に表すことができます。
上の線分図の辺ＨＤの長さが比の２、辺ＦＤの長さが比の１なので、辺ＨＦの長さは比の２－１＝１になります。
また、辺ＨＡと辺ＡＦの長さはそれぞれ辺ＨＦの半分なので、どちらも比の１÷２＝０.５と表せます。
このとき、辺ＡＤ＝辺ＡＦ＋辺ＦＤなので、辺ＡＤの長さを比で表すと０.５＋１＝１.５となります。
そして、辺ＢＣの長さは辺ＡＤの長さと等しい(どちらも長方形の横の長さ)ので、辺ＢＣの長さも比の１.５と表せます。
つまり比の１.５が辺ＢＣの長さである２ｍにあたるので、比の１にあたる長さは２ｍ÷１.５＝３分の４ｍになります。
求めたいのは辺ＡＦの長さ(比の０.５)なので、３分の４÷２＝３分の２ｍになります。
PR
