吉田商店では、Ａ、Ｂ、Ｃ３種類の商品を倉庫に保管しています。ある日の倉庫にあるＡ、Ｂ、Ｃの個数の比は５：４：３でした。その中からＡをその個数の２０％、Ｂを８個、Ｃを１０個取り出し、さらに、Ａ、Ｂ、Ｃとも同じ個数を取り出しました。
このとき、倉庫に残っていたＡとＢの個数の和は８８個、ＢとＣの個数の比は２：１になっていました。
(１)
倉庫に残っていたＡとＢの個数の差は( )個です。
(２)
Ａ、Ｂ、Ｃとも同じ個数を取り出しましたが、その個数は( )個です。
※ 解説を見たい場合は、下の「解説はこちらから」をクリック！
(１)
Ｃはこの問題には使わないので、とりあえず冷凍庫にでもしまっておいて、まずはＡとＢの関係だけに注目してみましょう。
最初のＡとＢの個数の比は、Ａ：Ｂ＝⑤：④です。
Ａは１回目にその２０％を取り出すので、残りは⑤×０.８＝④となり、この時点ではＢの個数と等しくなります。
Ｂは１回目に８個取り出すので、残りは④－８個と表せます。
このとき、１回目の作業の後のＡとＢの残りを線分図に表すと、次のようになります。
上の図のように、１回目の作業後のＡとＢの残りは８個差になっています。そして、２回目の作業ではＡとＢの両方から同じ個数ずつ取り出すので、この差は変わらないはずです(次の図)。
以上から、２回目の作業の後、倉庫に残っていたＡとＢの個数の差は８個になります。
※ この答えは、当然次の問題のヒントになっているはずです。
(２)
まずは２回目の作業後、ＡとＢはそれぞれ何個残っているのかを求めてみます。
２回目の作業後、ＡとＢの個数差は８個、個数の合計は８８個なので、次のような和差算の線分図に表すことができます。
上の図から、２回目の作業後のＡの残りは(８８＋８)÷２＝４８個、そしてＢの残りは４８－８＝４０個になります。
ではそろそろＣが必要な段階になってきたので、冷凍庫から取り出してレンジでチン！してあげましょう。
２回目の作業後、ＢとＣの残りの個数の比はＢ：Ｃ＝２：１、Ｂの残りの個数は４０個であることが分かっているので、Ｃの残りの個数を？個とおくと、
Ｂ：Ｃ＝２：１＝４０個：？個 ？個＝１×４０÷２＝２０個になります。
また、最初のＢとＣの個数の比はＢ：Ｃ＝４：３なので、そこから２回の作業の流れを図に表すと、次のようになります。
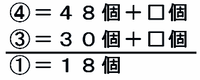
このとき、Ｂの最初の個数である④に戻すためには、残りの４０個に□個と８個を返してあげればいいので、④＝４０個＋□個＋８個＝４８個＋□個と表せます。
また、Ｃを最初の個数である③に戻すためには、残りの２０個に□個と１０個を返してあげればいいので、③＝２０個＋□個＋１０個＝３０個＋□個と表せます。
この２つの式を、次の図のように消去算っぽく計算すると、比の①＝１８個であることが分かります。
このとき、比の③は１８×③＝５４個なので、５４個＝３０個＋□個となり、２回目に取り出した個数は５４－３０＝２４個だと分かります。
PR
