下の図１、図２のように、長方形ＡＢＣＤの辺ＣＤの上に点Ｅがあります。点Ａと点Ｅを直線でつなぎ、ＡＥの上にＦＥ＝ＦＢとなるような点Ｆをとると、ＡＥとＦＢは直角に交わりました。このとき、次の各問いに答えなさい。
(１) 図１のように、ＦＣ＝５㎝のとき、四角形ＢＣＥＦの面積は何㎠ですか。
(２) 図２のように、ＡＦ＝２㎝、ＦＥ＝４㎝のとき、四角形ＡＢＣＤの面積は何㎠ですか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、四角形ＢＣＥＦは三角形ＦＢＣと三角形ＦＣＥの２つからできています。
つまりこの２つの三角形の面積の和を求めてしまえばＯＫなので、パズル感覚で解決していきます。
まずは次の図のように三角形ＦＣＥを切り取り、ＦＥとＦＢが重なるようにしてくっつけて、三角形ＦＧＣを作ります。
これは辺ＦＥと辺ＦＢが同じ長さだからこそできる技ですね。
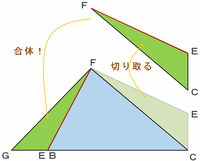
このとき、下の図の角アと角イの合計はもともと９０度だったので、角アと角ウの合計も９０度になります。
また、辺ＦＧはもともと辺ＦＣなので、この２つの辺は長さが等しくなっています。
辺ＦＧ＝辺ＦＣ、角ＧＦＣ＝９０度ということは、三角形ＦＧＣは直角二等辺三角形ですね。
しかも辺ＦＣ＝５㎝ということも分かっているので、求める面積は５×５÷２＝１２.５㎠になります。
(２)
これもさっきと同じようにパズル感覚で解ける問題です。
まずは三角形ＡＥＤを切り取り、それを次の図のように辺ＡＤと辺ＢＣが重なるようにくっつけると、底辺が２＋４＝６㎝の平行四辺形ができます。
この平行四辺形の高さにあたる辺ＦＢは辺ＦＥと長さが等しいので４㎝です。
したがって、求める面積は６×４＝２４㎠になります。
PR
