次の図の位置に１辺が６㎝の正方形ＡＢＣＤと長方形ＰＱＲＳがあり、正方形ＡＢＣＤの辺ＡＤに沿って長方形ＰＱＲＳが右の方へすべっていきます。辺ＰＱの真ん中の点Ｍが頂点Ｄに到着したら、長方形は点Ｍを中心に時計回りに点Ｑが辺ＣＤに重なるまで回転します。そして今度は辺ＣＤに沿って下の方まですべっていきます。
※ 画像はクリックすると拡大します。
次に点Ｍが頂点Ｃに到着したら、同じように点Ｍを中心に時計回りに点Ｑが辺ＢＣに重なるまで回転します。このようにして長方形ＰＱＲＳが正方形ＡＢＣＤの外側を１周したとき、次の問いに答えなさい。ただし、円周率は３.１４とします。
(１)
点Ｐが動く部分の長さを求めなさい。
(２)
長方形ＰＱＲＳが動いたあとはどのような図形になりますか。斜線で示しなさい。また、その面積を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
長方形ＰＱＲＳの中点Ｍが正方形の頂点Ｄまで進むと、次の図のように、長方形は点Ｄを中心として時計回りに９０度回転します。
そのときに点Ｐが動いてできる曲線は、半径３㎝で中心角９０度のおうぎ形の孤になります。
※ 画像はすべて、クリックすると拡大します。
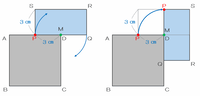
また、頂点Ｄで９０度回転した後の長方形ＰＱＲＳは、次の図のように点Ｍが正方形の頂点Ｃに来るまで下へまっすぐ進みます。
そのとき、点Ｐも下へまっすぐ３×２＝６㎝移動し、その後は頂点Ｃを中心として時計回りに９０度回転します。
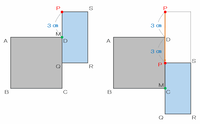
長方形ＰＱＲＳが正方形のまわりを１周するとき、「時計回りに９０度回転」と「まっすぐ６㎝進む」をそれぞれ４回ずつ行います。
そのときに点Ｐが動いた線は、次の図のように
・半径３㎝、中心角９０度のおうぎ形の孤が４本(青色)
・長さ６㎝の直線が４本(オレンジ色)
の２種類に分けられます。
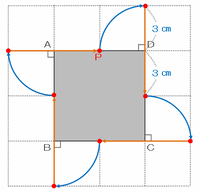
上の図の青い４本の孤(つまり円１個分)の長さの合計は３×２×３.１４＝１８.８４㎝、そして長さ６㎝の直線が４本で６×４＝２４㎝なので、点Ｐが動いた長さの合計は１８.８４＋２４＝４２.８４㎝です。
(２)
長方形ＰＱＲＳが次の図のように頂点Ｄで９０度回転するとき、点Ｓは青い矢印のように、そして点Ｒはオレンジ色の矢印のようにそれぞれ孤を描きます。
その２つの孤をつなげるとちょうど半円ができるのですが、今のところその半円の半径の長さは分かっていません。
※ というか、その長さは最後まで分からないままです。
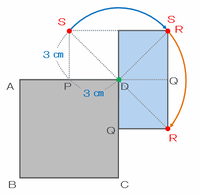
次の図の緑色の三角形ＳＤＲは底辺をＳＲ＝６㎝とすると高さは３㎝なので、その面積は６×３÷２＝９㎠です。
また、ＳＤＲは角ＳＤＲが直角で、辺ＤＳとＤＲの長さが等しい直角二等辺三角形なので、辺ＤＳとＤＲの長さをそれぞれ□㎝とおくと、三角形ＳＤＲの面積を求める式は□×□÷２＝９㎠と表せます。
したがって、「□×□」の答えは９×２＝１８になります。
上の図の□㎝は、ちょうど青色やオレンジ色の孤の半径にあたるので、その２つをつなげた半円の面積を求める式は「□×□×３.１４÷２」と表せます。
その式の「□×□」の部分にさっき求めた１８をあてはめて面積を求めると、１８×３.１４÷２＝２８.２６㎠となります。
長方形ＰＱＲＳが正方形のまわりを１周するとき、次の図のように「青い半円」と「緑色の直角二等辺三角形」がそれぞれ４個ずつできるので、その部分を斜線で示せばＯＫです。
また、青い半円４個の面積は２８.２６×４＝１１３.０４㎠、そして緑色の直角二等辺三角形４個の面積は９×４＝３６㎠なので、通過した面積の合計は１１３.０４＋３６＝１４９.０４㎠になります。
PR
