次の図の平行四辺形ＡＢＣＤにおいて、直線ＢＤ上にＢＥ：ＥＤ＝３：５となるように点Ｅをとり、直線ＡＥ上にＡＦ：ＦＥ＝３：２となるように点Ｆをとりました。平行四辺形ＡＢＣＤの面積が１４４㎠であるとき、三角形ＢＣＦの面積は何㎠ですか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
次の図の三角形ＡＢＥとＡＥＤは高さが同じで、底辺ＢＥとＥＤの長さの比が３：５なので、面積比も底辺比と同じく３：５になります。
また、三角形ＡＢＤの面積は平行四辺形ＡＢＣＤの半分にあたる１４４÷２＝７２㎠なので、それを３：５に比例配分して三角形ＡＢＥとＡＥＤの面積をそれぞれ求めてみると、
・三角形ＡＢＥ→７２×８分の３＝２７㎠
・三角形ＡＥＤ→７２×８分の５＝４５㎠
となります。
※ 画像はすべて、クリックすると拡大します。
また、次の図の三角形ＥＢＣとＥＣＤも高さが同じで底辺比がＢＥ：ＥＤ＝３：５なので、三角形ＥＢＣの面積は２７㎠、ＥＣＤの面積は４５㎠になります。
次の図の三角形ＡＥＤとＥＢＣは底辺ＡＤとＢＣの長さが同じなので、面積比と高さの比が等しくなります。
三角形ＡＥＤとＥＢＣの面積比は４５㎠：２７㎠＝５：３なので、この２つ三角形の高さの比もそれと同じく５：３になります。
次の図のように、三角形ＡＥＤの高さの比は５、そして辺ＡＦとＦＥの長さの比の合計も３＋２＝５で比の合計がそろっているので、緑色の三角形ＦＢＣの高さは比の３＋２＝５と表せます。
※ 赤い比の３と青い比の２を足すと、三角形ＦＢＣの高さの比が求められます。
つまり次の図のように、三角形ＡＥＤとＦＢＣは底辺ＡＤとＢＣの長さが等しく、高さの比も５で同じです。
底辺と高さが等しければ面積も同じはずなので、三角形ＦＢＣの面積はＡＥＤと同じく４５㎠です。
【補足】
実は最初から上の説明のような解き方を思いついたわけじゃなくて、次の図のように三角形ＦＢＣの内部を３つの三角形に分けてそれぞれの面積を求めてみたら答えが４５㎠になって、それが三角形ＡＥＤの面積と同じだったからいろいろ考えてみただけの話なんです(笑)
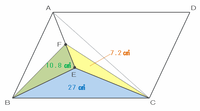
上の図の三角形ＥＢＣとＡＢＥはどちらも２７㎠、そしてＡＦ：ＦＥ＝３：２なので、三角形ＦＢＥの面積は２７×５分の２＝１０.８㎠です。
※ 三角形ＡＢＥの面積を３：２に比例配分。
また、補助線ＡＣを引いて平行四辺形を二等分すると、三角形ＡＢＣの面積は１４４÷２＝７２㎠なので、三角形ＡＥＣの面積は７２－(２７＋２７)＝１８㎠です。
※ 三角形ＡＥＣ＝ＡＢＣ－(ＡＢＥ＋ＥＢＣ)
三角形ＦＥＣの面積はＡＥＣの面積を３：２に比例配分すれば求められるので、１８×５分の２＝７.２㎠です。
以上から、三角形ＦＢＣの面積は２７＋１０.８＋７.２＝４５㎠になります。
雑に説明するとこんな感じです。さっきの解き方がいまいちピンとこない場合は、別にこちらの解き方でもいいんじゃないかなー、と思う今日この頃ですが、三角形ＡＥＤの高さの比と辺ＡＥの長さの比をどちらも５でそろえてくれた問題製作者の気持ちを考えると、個人的にはさっきの解き方を優先したくなりました。
PR
