図１は、長方形ＡＢＣＤに直角三角形ＥＢＣを重ねた図形です。この長方形の周上を、点Ｂから一定の速さで点Ｃ、Ｄを通って点Ａまで動く点Ｐがあります。図２のグラフは、点Ｐが点Ｂを出発してからの時間と、三角形ＥＣＰの面積との関係を表したものです。これについて、次の問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１) 図２のアにあてはまる数を答えなさい。
(２) 辺ＥＡと辺ＥＢの長さの比を最も簡単な整数を使って答えなさい。
(３) 点Ｐの動く速さは毎秒何㎝ですか。
(４) 図２のイにあてはまる数を答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずはスタートから５秒後、ア秒後、１１秒後、１３秒後などのときに三角形ＥＣＰがどのような形になっているのかを確認してみます。
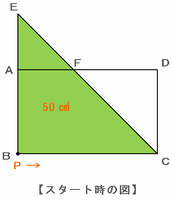
【スタート時の三角形ＥＣＰ】
点ＰがＢを出発するときの三角形ＥＣＰは次の図のような直角三角形になっており、面積はグラフから５０㎠であることも分かります。
この後、点ＰがＣへと近づくにつれて三角形ＥＣＰの面積はどんどん小さくなっていきます。
※ 画像はすべて、クリックすると拡大します。
【スタートから５秒後の三角形ＥＣＰ】
スタートから５秒後に点ＰはＣへ到着するため、そのときのＥＣＰは次の図のように直線になってしまいます。
この後、点ＰはＤに向かって進路を変え、三角形ＥＣＰの面積が少しずつ増えていきます。
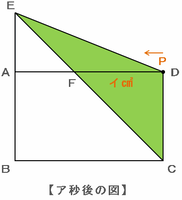
【スタートからア秒後の三角形ＥＣＰ】
スタートからア秒後に点ＰはＤへ到着し、三角形ＥＣＰは底辺がＣＰ、高さがＤＡの三角形になります。
また、そのときの面積がグラフの縦じくにあるイにあたります。
この後、点ＰがＦに近づくにつれて三角形の面積は少しずつ減っていきます。
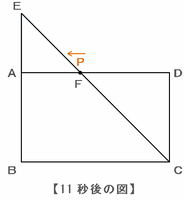
【スタートから１１秒後の三角形ＥＣＰ】
スタートから１１秒後に点ＰはＦへ到着するため、そのときのＥＣＰは次の図のように再び直線になります。
この後、点ＰはＡに向かって進み、三角形ＥＣＰの面積が少しずつ増えていきます。
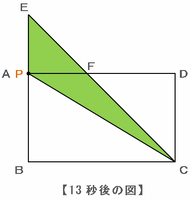
【スタートから１３秒後の三角形ＥＣＰ】
スタートから１３秒後に点ＰはＡへ到着し、三角形ＥＣＰは底辺がＥＰ、高さがＢＣの三角形になります。
これまでに確認したことをまとめてみると、点ＰはＢＣ間を５秒間で進み、その後はＣＤ間とＤＡ間を進んでＡに着きます。
このとき下の図のように、ＢＣ間とＤＡ間は同じ長さなので、点ＰがＤＡ間を進むのにかかった時間も５秒であることが分かります。
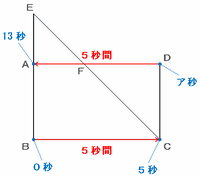
Ａに着いたのはスタートから１３秒後、Ｄを出発するのはその５秒前なので、グラフのアには１３－５＝８があてはまります。
(２)
点ＰはＡＦ間を１３－１１＝２秒、ＦＤ間を１１－８＝３秒かけて進むので、辺ＡＦと辺ＦＤの長さの比はＡＦ：ＦＤ＝２：３になります。
また、次の図の三角形ＥＡＦと三角形ＣＤＦは８の字相似になっているので、辺ＥＡと辺ＤＣの長さの比も２：３だと分かります。
このとき、下の図の辺ＡＢの長さは辺ＤＣと同じなので、こちらも比の３と表すことができます。
つまり、辺ＥＡの長さが比の２のとき、辺ＥＢの長さは比の２＋３＝５と表せるので、辺ＥＡと辺ＥＢの長さの比は２：５になります。
(３)
次の図の辺ＥＢの長さの比は⑤、そして辺ＢＣの長さも比の⑤なので、三角形ＥＢＣは直角二等辺三角形になります。
また、三角形ＥＢＣの面積はグラフから５０㎠であることが分かっているので、辺ＥＢと辺ＢＣの長さを□㎝とおくと、□×□÷２＝５０㎠という式ができます。
このとき、□×□の答えは５０×２＝１００になるので、□には１０があてはまります。
つまり、辺ＥＢと辺ＢＣの長さは次の図のようにどちらも１０㎝になるのですが、辺ＢＣは点Ｐが最初の５秒間で進んだ距離にあたるので、速さは１０÷５＝毎秒２㎝になります。
(４)
グラフのイには、点Ｐがスタートしてから８秒後の三角形ＥＣＰの面積があてはまります。
下の図の辺ＢＣの長さは１０㎝、そして辺ＣＤの長さは毎秒２㎝の点Ｐが８－５＝３秒間で進んだ距離なので２×３＝６㎝になります。
つまり８秒後の三角形ＥＣＰの面積は６×１０÷２＝３０㎠なので、グラフのイには３０があてはまります。
PR
