次の図１のような、高さが８㎝の台形ＡＢＣＤがあります。点Ｐは点Ａを出発して、秒速２㎝で辺ＡＤ上を何回も往復します。
※ 画像はすべて、クリックすると拡大します。
図２は、点Ｐ、Ｑが出発してからの時間と４点Ａ、Ｂ、Ｑ、Ｐで囲まれる図形の面積の関係をグラフに表したものです。このとき、次の問いに答えなさい。
(１) ３秒後の図形の面積は何㎠ですか。
(２) 点Ｐと点Ｑが出発しました。次の①～③の中から正しいものを１つ選び、番号で答えなさい。
① 点Ｑが点Ｃに着くより先に、点Ｐが点Ｄに着く。
② 点Ｐが点Ｄに着くより先に、点Ｑが点Ｃに着く。
③ 点Ｐが点Ｄに着くのと、点Ｑが点Ｃに着くのが同時である。
(３) 辺ＢＣの長さは何㎝ですか。
(４) 図２のグラフのアとイの値はいくらですか。
(５) 出発した後、４点Ａ、Ｂ、Ｑ、Ｐで囲まれる図形の面積が初めて０になるのは何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
３秒後の辺ＡＰの長さは２×３＝６㎝、辺ＢＱの長さは３×３＝９㎝なので、台形ＡＢＱＰの面積は(６＋９)×８÷２＝６０㎠になります。
(２)
次のグラフの赤い部分は、３秒後と４秒後に「点ＰがＤに着いた」または「点ＱがＣに着いた」ことを表しています。
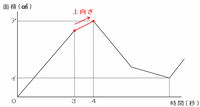
もし「点ＱがＣに着いた」が「点ＰがＤに着いた」よりも先の場合、その後は
・点Ｐは右へ秒速２㎝で進む→台形ＡＢＱＰの面積はちょっと増える
・点Ｑは左へ秒速３㎝で進む→台形ＡＢＱＰの面積はたくさん減る
・増える量より減る量の方が多い
ことから、グラフの赤い線は下向きになるはずです。
しかし実際には、グラフの赤い直線は上向きになっていることから、
・先に点ＰがＤに着いて左へ秒速２㎝で引き返し始めた→台形ＡＢＱＰの面積はちょっと減る
・点Ｑは右へ秒速３㎝で進み続ける→台形ＡＢＱＰの面積はたくさん増える
・減る量より増える量が多い
という流れになっていることが分かります。
以上から、答えは「点Ｐが先にＤへ着いた」ことを表す①になります。
(３)
さっきのグラフから、３秒後には点ＰがＤに着き、４秒後には点ＱがＣに着いたことが分かります。
したがって、辺ＡＤの長さは２×３＝６㎝、そして辺ＢＣの長さは３×４＝１２㎝になります。
(４)
次のグラフを使って、点ＰとＱの動きを確認してみると、
・グラフの①→点ＰがＤに到着。その後は点Ｐが左へ引き返し、点Ｑは右へ進み続けるので、面積はちょっとずつ増える。
・グラフの②→点ＱがＣに到着。その後は点Ｑも左へ引き返し始めるので、面積は勢いよく減っていく。
・グラフの③→点ＰがＡに到着。その後は点Ｐが右へ進み始めるが、点Ｑは相変わらず左へ進んでいるので、面積はちょっとずつ減る。
・グラフの④→点ＱがＢに到着。その後は点Ｑも右へ進むので、面積は勢いよく増え始める。
という流れになっています。
グラフのアはスタートから４秒後の台形ＡＢＱＰの面積があてはまります。
点Ｐは４秒間で２×４＝８㎝進むので、次の図のようにＤから左へ８－６＝２㎝進んだ地点にいます。
また、点ＱはちょうどＣに到着したときなので、台形ＡＢＱＰの面積は(４＋１２)×８÷２＝６４㎠になります。
グラフのイは点ＱがＢに戻ってきたときの様子を表しています。
点ＱがＢへ戻るまでにかかる時間は１２×２÷３＝８秒なので、その間に点Ｐは２×８＝１６㎝進みます。
つまり、点ＰはＡから右へ１６－６×２＝４㎝進んだ地点にいる(ＡＤ間を１往復してからさらに４㎝進んだ)ので、そのときのＡＢＱＰは四角形ではなく三角形ＡＱＰになります。
三角形ＡＱＰは直角三角形なので、面積は４×８÷２＝１６㎠です。
以上から、グラフのアには６４が、そしてイには１６がそれぞれあてはまります。
(５)
ＡＢＱＰの面積が０になるのは、点Ｐ、ＱがＡとＢへ同時に戻ってきたときです。
点ＰがＡに戻るのは６×２÷２＝６秒ごと、点ＱがＢに戻るのは１２×２÷３＝８秒ごとなので、６と８の最小公倍数である２４秒後のとき、ＡＢＱＰの面積は初めて０になります。
PR
