次の図のように、直線Ｌの上に直角二等辺三角形があります。点Ｐは辺ＡＢの真ん中の点です。直角二等辺三角形ＡＢＣが、アの位置からイの位置まで、直線Ｌ上をすべらないように転がりました。円周率を３.１４として、次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
点Ｐが動いた後の線の長さは何㎝ですか。
(２)
点Ｂが動いた後の線と直線Ｌとで囲まれた部分の面積は何㎠ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
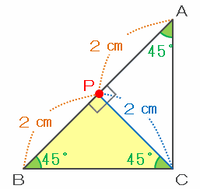
次の図のように、辺ＡＢの真ん中の点ＰからＣへ直線を引くと、
・角ＰＢＣはもともと４５度
・角ＰＣＢは角ＡＣＢの半分なので９０÷２＝４５度
・角ＢＰＣは１８０－４５×２＝９０度
となることから、三角形ＰＢＣは直角二等辺三角形となり、辺ＰＣの長さはＰＢと同じく２㎝であることが分かります。
※ 画像はすべて、クリックすると拡大します。
【頂点Ｃを中心として回転するとき】
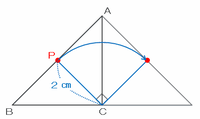
次の図のように、頂点Ｃを中心として三角形ＡＢＣを右へ９０度回転させるとき、点Ｐが通る線は半径２㎝で中心角９０度のおうぎ形の孤になります。
【頂点Ｂを中心として回転するとき】
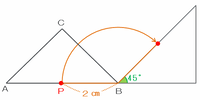
次の図のように、頂点Ｂを中心として三角形ＡＢＣを右へ１８０－４５＝１３５度回転させるとき、点Ｐが通る線は半径２㎝で中心角１３５度のおうぎ形の孤になります。
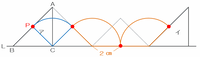
三角形ＡＢＣが次の図のアからイの位置まで回転しながら移動するとき、点Ｐが通った線は
・半径２㎝で中心角９０度のおうぎ形の孤が１つ(青色)
・半径２㎝で中心角１３５度のおうぎ形の孤が２つ(オレンジ色)
になるので、その３つの孤の中心角の合計は９０＋１３５×２＝３６０度になります。
つまり、点Ｐが動いた長さは半径２㎝の円１個分の周りの長さと等しいので、答えは２×２×３.１４＝１２.５６㎝になります。
(２)
直角二等辺三角形ＡＢＣが次の図のようにアからイへ回転しながら移動するとき、点Ｂは図の青色とオレンジ色の孤を描きながら進みます。
したがって、求める面積は下の図の青色とオレンジ色のおうぎ形、そして緑色の直角二等辺三角形の３つに分けられるので、ここからはそれぞれの面積を１つずつ求めてみます。
【オレンジ色のおうぎ形の面積を求める】
オレンジ色のおうぎ形の半径は直角二等辺三角形ＡＢＣの辺ＡＢの長さと等しく４㎝、そして中心角は１８０－４５＝１３５度です。
したがって、その面積は４×４×３.１４×(３６０分の１３５)＝１８.８４㎠になります。
【緑色の直角二等辺三角形の面積を求める】
緑色の直角二等辺三角形の面積は、最初の位置にあるアのときの面積を求めればＯＫなので、次の図のように底辺が４㎝、高さが２㎝と考えれば、面積は４×２÷２＝４㎠になります。
【青色のおうぎ形の面積を求める】
次の図の直角二等辺三角形ＡＢＣの面積は４㎠なので、辺ＡＣやＢＣの長さを□㎝とおくと、その面積を求める式は□×□÷２＝４㎠と表せます。
したがって、□×□の答えは４×２＝８となることが分かります。
次の青色のおうぎ形の面積を求める式は□×□×３.１４÷４と表せます。
この式の□×□の部分は８であることが分かっているので、面積は８×３.１４÷４＝６.２８㎠になります。
以上から、求める面積は６.２８＋４＋１８.８４＝２９.１２㎠になります。
PR
