図のような縦６ｍ横１１ｍの長方形から縦３ｍ横６ｍの長方形を、辺が平行になるようにくりぬいた一枚の板があります。太郎君がＡを毎秒８０㎝の速さでＢに向かって出発した３秒後、次郎君はＤを太郎君と同じ速さでＣに向かって出発しました。このとき、次の( )に適当な数をいれなさい。
※ 画像はクリックすると拡大します。
(１)
太郎君が出発してから５秒後に太郎君と次郎君を結んだ直線で板を切ったとき、小さい板と大きい板の面積の比を最も簡単な整数の比で表すと、( )：( )になります。
(２)
太郎君が出発してから( )秒後に太郎君と次郎君を結んだ直線で板を切ると、板は２等分されます。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずはくりぬいた長方形の上下と左横のすきまの幅を確認しておくと、下の図の青い矢印は４－３＝１ｍ、赤い矢印は６－４＝２ｍ、緑の矢印は１１－９＝２ｍになります。
※ 画像はすべて、クリックすると拡大します。
長方形ＡＢＣＤの面積は６×１１＝６６㎡、くりぬいた長方形の面積は３×６＝１８㎡なので、残った板の面積は６６－１８＝４８㎡になります。
太郎君がＡを出発してから３秒後に、次郎君はＤからＣへ向けて出発します。
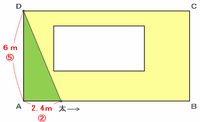
そのとき、太郎君はＡから０.８×３＝２.４ｍはなれた場所にいるので、次郎君のいるＤも含めた３点を結ぶと、次の図のような緑色の直角三角形ができます。
また、この三角形の長さの比は、高さ：底辺＝６ｍ：２.４ｍ＝⑤：②になっています。
太郎君のスタートから５秒後、太郎君はＡから０.８×５＝４ｍ、そして次郎君はＤから０.８×(５－３)＝１.６ｍの地点にいます。
そのとき、２人のいる地点を直線で結んで板を切断すると、次の図のように台形(図のアとイ)から青い三角形(図のイ)をくりぬいた形ができます。
※ イがちょうど三角形になる理由は、後の【補足】を参考にしてください。
左側にできた台形の面積は、(１.６＋４)×６÷２＝１６.８㎡です。
また、この青い三角形はさっきの緑色の三角形と相似になっているので、高さと底辺の比は⑤：②のはずです。
青い三角形の底辺を□ｍとおくと、３ｍ：□ｍ＝⑤：②という比ができるので、□には３ｍ×②÷⑤＝１.２ｍがあてはまります。
つまり青い三角形の面積は１.２×３÷２＝１.８㎡になるので、上の図のアの面積は１６.８－１.８＝１５㎡になります。
また、下の図の左側が１５㎡、くりぬいた後の板全体の面積が４８㎡なので、右側の面積は４８－１５＝３３㎡になります。
したがって、小さい板と大きい板の面積比は、小：大＝１５：３３＝５：１１になります。
【補足】
太郎君がＡを出発してから５秒後、次郎君は次の図のようにＤから１.６ｍ進んだ地点にいます。
このとき、下の図の青色と緑色の三角形はどちらも高さと底辺の長さの比が⑤：②になっています。
緑色の三角形の底辺を□ｍとおくと、１ｍ：□ｍ＝⑤：②と表せるので、□には１ｍ×②÷⑤＝０.４ｍがあてはまります。
つまり、下の図の赤い点は左はしから１.６＋０.４＝２ｍの地点にあるので、ちょうどくりぬいた長方形の左上と重なります。
(２)
太郎君がＡを出発して５秒後からしばらくの間は、次の図のように左側の板の面積がアとイの平行四辺形の分だけ一定の割合で増えていきます。
たとえば５秒後から６秒後までの１秒間で、左側の板の面積には新たに青い平行四辺形アとイの面積が加わります。
アとイの面積の合計は０.８×１＋０.８×２＝２.４㎡なので、下の図の左側の板の面積は、５秒後から１秒たつごとに２.４㎡ずつ増えていきます。
くりぬいた後の板全体の面積は４８㎡、その半分は４８÷２＝２４㎡なので、上の図の左側の板の面積が２４－１５＝９㎡増えれば、板の面積がちょうど２等分されます。
９÷２.４＝３.７５秒なので、板の面積がちょうど２等分されるのは、太郎君がＡを出発してから５＋３.７５＝８.７５秒後になります。
PR
