次の図のような三角すいがあります。辺ＣＤの真ん中の点をＥ、ＢＥ＝８㎝とします。辺ＡＢを軸にしてこの立体を１回転させるとき、次の問いに答えなさい。ただし、円周率は３.１４とします。
※ 画像はクリックすると拡大します。
(１) 三角形ＡＢＣが１回転してできる立体の体積を求めなさい。
(２) 三角形ＡＣＤが１回転してできる立体の体積を、式を書いて求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
三角形ＡＢＣが辺ＡＢを軸として１回転すると、次の図のような円すいができあがります。
※ 画像はすべて、クリックすると拡大します。
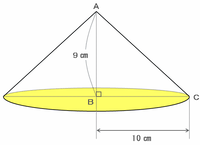
この円すいは底面の円の半径が１０㎝、高さは９㎝なので、体積は１０×１０×３.１４×９÷３＝９４２㎤になります。
(２)
結論から言うと、辺ＡＢを軸にして三角形ＡＣＤを１回転させてできる立体は、とんがりコーンのように内部がくり抜かれた円すいになります。
また、次の図を使って頂点Ｂから三角形ＡＣＤの底辺である辺ＣＤまでの最短ルートと最長ルートを確認しておくと、
・最短ルート→頂点ＢからＥまでを直線で結んだときの８㎝
・最長ルート→頂点ＢからＣまたはＤまでを結んだときの１０㎝
となっています。
このとき、次の図の「三角形ＡＢＣを１回転させてできる円すいの体積」から「三角形ＡＢＥを１回転させてできる円すいの体積」を引くと、とんがりコーンの部分の体積が求められます。
「三角形ＡＢＣを１回転させてできる円すいの体積」は、さっきの問題で求めたように９４２㎤です。
また、「三角形ＡＢＥを１回転させてできる円すいの体積」は、８×８×３.１４×９÷３＝６０２.８８㎤です。
したがって、この問題で求めたい「とんがりコーン」の部分の体積は、９４２－６０２.８８＝３３９.１２㎤になります。
【補足】
完成した立体図は次のような感じになります。黄色い部分が「とんがりコーン」、青色がくり抜かれた内部を表しています。
PR
