１以上１００以下の２つの整数ｍ，ｎ(ただし、ｍはｎより大きい)について次のような操作をします。
操作① ｍを割られる数、ｎを割る数として割り算を行い、商と余りを求めます。
操作② 前の割り算の割る数を割られる数、余りを割る数として割り算を行い、商と余りを求めます。
これを、余りがなくなるまでくり返します。このとき、求めた商と余りをそれぞれ、順番に→を使って書くことにします。
次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
ｍ＝６７、ｎ＝９のとき、商を→を使って書きなさい。
(２)
ｍ＝ア、ｎ＝イのとき、商が「１→２→１→２」で、余りが「ウ→エ→１→なし」となりました。ア～エにあてはまる数はそれぞれいくつですか。
(３)
ｍ＝オ、ｎ＝カのとき、商が「１→２→１→２」で、余りが「キ→ク→２→なし」となりました。オ～クにあてはまる数はそれぞれいくつですか。
(４)
ｍ＝ケ、ｎ＝コのとき、商が「１→２→１→２」となりました。ケとコにあてはまる整数の組(ケ・コ)は全部で何組ありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは「６７÷９」の計算からスタートして、問題文のルールの通りに余りがなくなるまで計算してみると、
① ６７÷９＝７余り４→「９」と「４」を移動
② ９÷４＝２余り１→「４」と「１」を移動
③ ４÷１＝４→割り切れたのでここで終了
のようになるので、商は「７→２→４」となります。
(２)
商が４つあるので、次の図のように割り算の式を４行用意し、すでに分かっている商や余りなどを書き込んでみます。
※ 画像はすべて、クリックすると拡大します。
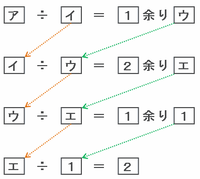
上の図には６個の空欄がありますが、オレンジ色や緑色の矢印を頼りにしていけば次のようにすべて埋めることができます。
上の図を利用して４行目から１行目へ向けて少しずつ逆算していくと・・・
・４行目→エ÷１＝２なので、エは２×１＝２
・３行目→ウ÷２＝１余り１なので、ウは２×１＋１＝３
・２行目→イ÷３＝２余り２なので、イは３×２＋２＝８
・１行目→ア÷８＝１余り３なので、アは８×１＋３＝１１
となることから、答えはア＝１１、イ＝８、ウ＝３、エ＝２です。
(３)
さっきの問題と同じように、すでに分かっている数字や矢印を頼りにして割り算の４行の式を埋めてみると次の図のようになります。
上の図を利用して４行目から１行目へ向けて少しずつ逆算していくと・・・
・４行目→ク÷２＝２なので、クは２×２＝４
・３行目→キ÷４＝１余り２なので、キは４×１＋２＝６
・２行目→カ÷６＝２余り４なので、カは６×２＋４＝１６
・１行目→オ÷１６＝１余り６なので、オは１６×１＋６＝２２
となることから、答えはオ＝２２、カ＝１６、キ＝６、ク＝４です。
(４)
とりあえず問題文に書いてある数字を穴埋めしてみても、下のように分からない部分が多すぎて逆算できません。
そこで、次の図のように４行目の式の「割る数」を①、他のマスをＡ～Ｃとおき、ケとコにあてはまる数を割合で求めてみると、
・４行目→Ｂ÷①＝２なので、Ｂは①×２＝②
・３行目→Ａ÷②＝１余り①なので、Ａは②×１＋①＝③
・２行目→コ÷③＝２余り②なので、コは③×２＋②＝⑧
・１行目→ケ÷⑧＝１余り③なので、ケは⑧×１＋③＝⑪
となることから、ケ：コ＝１１：８であることが分かります。
ケ：コ＝１１：８なので、ケは１１の倍数、コは８の倍数になります。
また、１００÷１１＝９余り１なので、１から１００までの整数の中にケの候補となる数字は９個あります。
以上から、ケとコの組み合わせは全部で９組になります。
【補足】
１００÷８＝１２余り４なので、１から１００までの整数の中にコの候補となる数字は１２個あります。
しかしケは９個しかないので、ケとコの組み合わせは９組しかできません。
PR
