図１のように、１本の直線の上に図形ＡＢＣＤＥＦと一辺が１０㎝の正方形ＧＨＩＪがあります。正方形ＧＨＩＪは動きませんが、図形ＡＢＣＤＥＦは直線の上を毎秒１㎝の速さで右へ動き、少しずつ正方形ＧＨＩＪと重なりながら通り抜けます。
図２のグラフは、２つの図形が重なり始めてからの時間と、重なった部分の面積の関係を表したものです。この図のように、４、１０、１２、１４秒後のそれぞれの時間で、グラフの角度が変化していきます。次の問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１)
辺ＥＤの長さを求めなさい。
(２)
グラフのア～エにあてはまる数を求めなさい。
(３)
重なった面積が４８㎠になるときは２回あります。２回目に４８㎠になるのは、２つの図形が重なり始めてから何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
グラフを見れば分かるように、最初の４秒間は重なる部分の面積の増え方が一定で、その後は面積の増え方が大きくなります。
そこで、まずは重なり始めてから４秒間の様子を次の図１から図３で表してみると、４秒後には図３のように辺ＦＥが辺ＧＨと重なる地点まで進みます。
※ 画像はすべて、クリックすると拡大します。
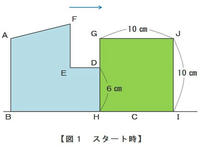
上の図３はスタートから４秒後の重なりを表しています。
図形ＡＢＣＤＥＦは毎秒１㎝で進むので、上の図３の辺ＥＤの長さは１×４＝４㎝になります。
(２)
グラフのアは、次の図のように図形ＡＢＣＤＥＦが正方形ＧＨＩＪを左から右へ完全に突き抜けるまでにかかる時間を表しています。
※ 画像はすべて、クリックすると拡大します。
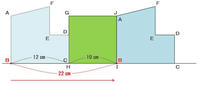
上の図を見れば分かるように、図形ＡＢＣＤＥＦが正方形ＧＨＩＪを左から右へ完全に突き抜けるとき、頂点Ｂは１２＋１０＝２２㎝移動します。
図形ＡＢＣＤＥＦは毎秒１㎝の速さで動くので、グラフのアには２２÷１＝２２秒があてはまります。
グラフのイのときに２つの図形が重なっている様子を図に表すと、次のようになります。
重なっている部分(黄色)の面積は、一辺１０㎝の正方形ＧＨＩＪから一辺４㎝の緑色の正方形の面積を引けば求められるので、イには１０×１０－４×４＝８４㎠があてはまります。
グラフのウのときは、下の図のように２つの図形の重なりが最大になります。
このとき、重なっている部分(黄色)の面積は、一辺１０㎝の正方形ＧＨＩＪから緑色の長方形の面積を引けば求められます。
上の図の辺ＨＣの長さは１２㎝、辺ＨＩの長さは１０㎝なので、辺ＩＣの長さは１２－１０＝２㎝です。
また、辺ＥＤの長さは４㎝なので、辺ＫＪの長さは４－２＝２㎝になります。
グラフのウには上の図の黄色い重なりの面積があてはまるので、答えは１０×１０－４×２＝９２㎠です。
グラフのエのときに２つの図形が重なっている様子を図に表すと、次のようになります。
重なっている部分(黄色)の辺ＢＩの長さは辺ＢＣと辺ＩＣの差にあたるので、１２－４＝８㎝であることが分かります。
したがって、エには１０×８＝８０㎠があてはまります。
(３)
次のグラフを見れば分かるように、重なりの面積が初めて４８㎠になるのはイの前、そして２回目はエの後にあります。
重なりの部分が２回目に４８㎠になるのは、次の図のように辺ＢＩの長さが４８÷１０＝４.８㎝のときです。
上の図の辺ＢＩが４.８㎝なら、辺ＨＢの長さは１０－４.８＝５.２㎝になります。
そのとき、頂点Ｂは重なり始めたときに比べて１２＋５.２＝１７.２㎝動いたことが分かるので、答えは１７.２÷１＝１７.２秒後になります。
PR
