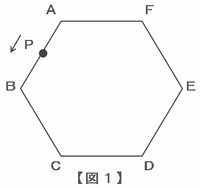
次の図１のような１辺が２㎝の正六角形ＡＢＣＤＥＦがあります。点Ｐは点Ａを出発して、反時計回りに毎秒１㎝の速さで正六角形の辺上を１周します。このとき、点Ｐが通過した部分と直線ＡＰで囲まれた多角形の面積について、点Ｐが動いた時間との関係を図２に表しています。次の各問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１)
点Ｐがちょうど点Ｃ上にあるときの多角形の面積をアとすると、点Ｐがちょうど点Ｄ上にあるときの多角形の面積はアの何倍か求めなさい。
(２)
点Ｐが点Ａを出発してから１周するまでの多角形の面積について、図２のグラフを完成させなさい。
(３)
点Ｑが点Ｐと同時に点Ａを出発して、時計回りに毎秒１㎝の速さで正六角形の辺上を進み、２点Ｐ、Ｑが出会ったところで止まります。このとき、２点Ｐ、Ｑが通過した部分と直線ＰＱで囲まれた多角形の面積が、正六角形ＡＢＣＤＥＦのちょうど３分の１になるのは、２点Ｐ、Ｑが点Ａを出発してから何秒後か求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
点ＰがＡから反時計回りに進むにつれて、点Ｐが通過した部分と直線ＡＰで囲まれた部分の面積は次の図のようにどんどん大きくなっていきます。
※ 画像はすべて、クリックすると拡大していきます。
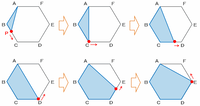
点ＰがちょうどＣに来たとき、青い部分の面積は次の図①のような二等辺三角形ＡＢＰになっています。
このとき、二等辺三角形ＡＢＰを下の図②のように辺ＢＨで切断し、三角形ＢＰＨを矢印のように移動させると、正三角形ＡＢＧができます。
また、正三角形ＡＢＧは正六角形ＡＢＣＤＥＦを６個の小さな正三角形に分けたときの１個分にあたります。
※ つまり、グラフのアは小さい正三角形１個分の面積を表しています。
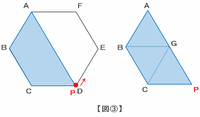
点ＰがちょうどＤに着いたとき、青い部分の面積は図③のような台形ＡＢＣＤになります。
下の図を見れば分かるように、この台形ＡＢＣＤは小さな正三角形ＡＢＧが３個くっついてできた形なので、点ＰがＣにいるときの青い部分の面積に比べて３÷１＝３倍になります。
(２)
点Ｐの進む速さは毎秒１㎝、正六角形の１辺の長さは２㎝なので、点Ｐは１辺を進むのにかかる時間は２÷１＝２秒です。
さっきの問題で点ＰがＤまで進んだときの青い部分の面積までは分かったので、ここからは点ＰがさらにＥ→Ｆ→Ｇと進んだときの青い部分の面積がどうなるのかを確認してみます。
【点ＰがＥまで進んだとき】
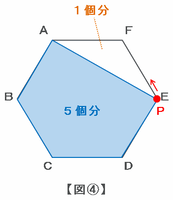
点ＰがＥまで進んだときの青色の部分は次の図④のような五角形になります。
この図の三角形ＦＡＥは小さい正三角形１個分の面積なので、青色の部分の面積は小さい正三角形の６－１＝５個分にあたります。
【点ＰがＦまで進んだとき】
点ＰがＦまで進んだとき、次の図⑤のように青色の部分が六角形全体に広がるので、青色の部分の面積は小さい正三角形の６個分になります。
【点ＰがＡに帰ってきたとき】
点ＰがＡに帰ってきたときも、青色の部分は次の図⑥のように六角形全体のままです。
ここで今までの流れをカンタンに振り返ってみると・・・
・点ＰがＣに着いたとき→青色の部分の面積は小さい三角形１個分
・点ＰがＤに着いたとき→青色の部分の面積は小さい三角形３個分
・点ＰがＥに着いたとき→青色の部分の面積は小さい三角形５個分
・点ＰがＦに着いたとき→青色の部分の面積は小さい三角形６個分
・点ＰがＡに着いたとき→青色の部分の面積は小さい三角形６個分のまま
となっているので、それらをグラフに表すと次の図のようになります。
(３)
点Ｐと点ＱはＡを同時に出発してどちらも毎秒１㎝で進むので、出発から２秒後には青い部分が次の図⑦のような二等辺三角形なっています。
上の図の青い部分の面積は小さい正三角形１個分、そして正六角形の３分の１の面積は小さい正三角形２個分なので、次の図⑧のように点Ｐと点Ｑがさらに進み、長方形ＢＰＱＦの面積が小さい正三角形１個分になるときを考えればＯＫです。
長方形ＢＰＱＦの面積が小さい正三角形１個分の面積と等しくなるときの辺ＢＰの長さを求めるため、次の図⑨のように３つの図形を並べて比較してみます。
小さい正三角形は底辺が２㎝、高さが①なので、面積は２×①÷２＝１と表せます。
一方、長方形ＢＰＱＦは底辺が□㎝、高さが②、そして面積は小さい正三角形と同じく１なので、面積を求める式は□×②＝１と表せます。
したがって、辺ＢＰの長さは１÷②＝０.５㎝であることが分かります。
つまり、青い部分の面積が正六角形全体の３分の１になるのは、次の図⑩のように点Ｐと点ＱがそれぞれＡから２＋０.５＝２.５㎝進んだときなので、２つの点が出発してから２.５÷１＝２.５秒後になります。
PR
