３つの数を小さい順に並べ、Ａ、Ｂ、Ｃとしたとき、Ａ、Ｂ、Ｃを全部たして３で割った数を＜Ａ、Ｂ、Ｃ＞で表します。
例えば、＜２、４、９＞＝(２＋４＋９)÷３＝５となります。
(１)
次の計算をしなさい。
＜＜１５、６５、９９１＞、＜０、９９０、１００９＞、＜１９３５、１９８５、２０１０＞＞
(２)
１から７までの７個の整数の中から異なる３つの整数を選び、小さい順にＡ、Ｂ、Ｃとします。このとき、＜Ａ、Ｂ、Ｃ＞が整数となるＡ、Ｂ、Ｃの選び方は何通りありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは３つのカッコの中をそれぞれ計算してみると、それぞれ次のようになります。
・＜１５、６５、９９１＞＝(１５＋６５＋９９１)÷３＝１０７１÷３
・＜０、９９０、１００９＞＝(０＋９９０＋１００９)÷３＝１９９９÷３
・＜１９３５、１９８５、２０１０＞＝(１９３５＋１９８５＋２０１０)÷３＝５９３０÷３
最終的にはこの３つをたしてから３で割ればＯＫなので、まずは「１０７１÷３」、「１９９９÷３」、「５９３０÷３」の３つの和を求めてみると・・・
１０７１÷３＋１９９９÷３＋５９３０÷３
＝(１０７１＋１９９９＋５９３０)÷３
＝９０００÷３
＝３０００
となります。
したがって、答えは３０００÷３＝１０００になります。
【補足】
１９９９と５９３０はどちらも３で割り切れないので、この方法を使わないと計算がちょっとややこしくなると思います。
(２)
３つの数Ａ、Ｂ、Ｃの和が３で割り切れる組み合わせを見つければＯＫです。
１から７までの３つの数の合計が３の倍数になる組み合わせのうち、Ａ＝１の場合を考えてみると、(Ａ・Ｂ・Ｃ)＝(１・２・３)、(１・２・６)、(１・３・５)、(１・４・７)、(１・５・６)の５組があります。
それらを次の図のように並べ、カッコの中にある３つの数にそれぞれ１ずつ足していくと、３の倍数になる組み合わせをすべて見つけることができます。
※ 画像はクリックすると拡大します。
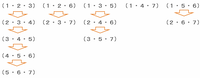
上の図から、＜Ａ、Ｂ、Ｃ＞にあてはまる組み合わせは全部で５＋２＋３＋１＋２＝１３通りになります。
【補足】
カッコの中にある３つの数の和が３の倍数であれば、それに１＋１＋１＝３を足しても３の倍数のまま変わりません。
ただし、この問題の場合は使える数が１から７までなので、３つの数のうちのどれかが７になった時点で終わりです。
PR
