下の図は、高さが縦や横の長さの２倍より長い直方体で、この直方体の辺に沿って２点Ｐ、Ｑが動きました。２点は同時にＡを出発し、点Ｐは毎秒２㎝の速さでＥ、Ｆを通ってＢまで、点Ｑは毎秒１㎝の速さでＤ、Ｃを通ってＢまで動き、同時に着きました。下のグラフは、Ｐ、ＱがＡを出発してからの時間と、三角形ＡＢＰと三角形ＡＢＱの面積の和の関係を表しています。次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) ＡＢ、ＡＤ、ＡＥの長さをそれぞれ求めなさい。
(２) ア、イの値を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは時間の経過とともに三角形ＡＢＰと三角形ＡＢＱの面積がどのように変化していくのかを確認しながら、辺ＡＤと辺ＡＥの長さを求めてみます。
【図１ スタートしてからしばらくの間】
次の図１のように、点ＰとＱがそれぞれＡを出発してからしばらくの間は、２つの三角形の面積がひたすら増えていくだけなので、面積の合計も勢いよく増えていきます。
※ 画像はすべて、クリックすると拡大します。
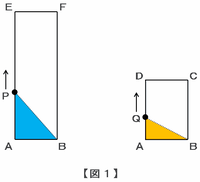
【図２ スタートしてから８秒後】
２つの点が出発してから８秒後、点Ｑは頂点Ｄに到着したため、三角形ＡＢＱの面積は次の図２のように最大になりました。
点Ｐはまだ頂点Ｅに到達していないので、三角形ＡＢＰの面積はもう少し増えるのですが、三角形ＡＢＱの面積が増えない分だけグラフの角度がゆるやかになります。
このとき、点Ｑは辺ＡＤ間を秒速１㎝で８秒間かけて進んだので、辺ＡＤの長さは１×８＝８㎝になります。
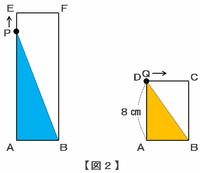
【図３ スタートしてから９秒後】
２つの点が出発してから９秒後、今度は点Ｐが頂点Ｅに到着したため、三角形ＡＢＰの面積は次の図３のように最大になりました。
ここからしばらくの間は、点Ｐが辺ＥＦ上を、そして点Ｑが辺ＤＣ上を移動しているので、２つの三角形の面積は最大のまましばらく変わらないことがグラフから読み取れます。
このとき、点Ｐは辺ＡＥ間を秒速２㎝で９秒間かけて進んだので、辺ＡＥの長さは２×９＝１８㎝になります。
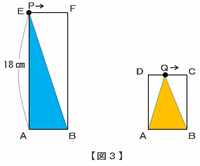
【辺ＡＢの長さを求める】
点Ｐは毎秒２㎝、点Ｑは毎秒１㎝で進んで同時にゴールするので(問題文に書いてあります)、２つの点が進んだ距離の比は点Ｐ：点Ｑ＝２：１になります。
このとき、点Ｐと点Ｑが進んだ距離をそれぞれ確認してみると・・・
点Ｐが進んだ距離→辺ＡＥ＋辺ＥＦ＋辺ＦＢだから、１８×２＝３６㎝と辺ＥＦ
点Ｑが進んだ距離→辺ＡＤ＋辺ＤＣ＋辺ＣＢだから、８×２＝１６㎝と辺ＤＣ
のようになります。
また、辺ＥＦと辺ＤＣはどちらも辺ＡＢの長さと等しいので、その長さを□㎝とおくと、点Ｐと点Ｑが進んだ距離の関係は次のような線分図に表すことができます。
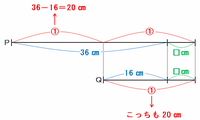
上の線分図の点Ｐと点Ｑの線にはどちらも「□㎝」があるので、２本の線の長さの差は３６－１６＝２０㎝です。
また、点Ｐが進んだ距離は②、点Ｑが進んだ距離は①なので、２本の線の長さの差は②－①＝①とも表せます。
つまり、上の線分図の比の①が２０㎝にあたるのですが、それは点Ｑが進んだ距離でもあるので、１６㎝と□㎝の合計も２０㎝になります。
以上から、辺ＡＢの長さ(辺ＤＣの長さと同じ)は２０－１６＝４㎝になります。
(２)
グラフのアは、秒速１㎝で進む点Ｑが辺ＡＤから辺ＤＣ、そして辺ＣＢを進むのにかかった時間を表しています。
さっきの問題で点Ｑが進んだ距離の合計は２０㎝であることが分かっているので、グラフのアには２０÷１＝２０があてはまります。
※ 解答欄には単位の「秒」は書かないように注意しましょう。
グラフのイは２つの三角形の面積が最大のときの面積の合計を表しています。
三角形ＡＢＰの面積の最大値は４×１８÷２＝３６㎠、そして三角形ＡＢＱの面積の最大値は４×８÷２＝１６㎠なので、イには３６＋１６＝５２があてはまります。
PR
