下図のような図形に、Ａ、Ｂ、Ｃ、Ｄ、Ｘの５つの地点があります。
地点間の道のりはそれぞれ、ＡからＢが２㎝、ＢからＣが１０㎝、ＣからＤが６㎝、ＤからＡが８㎝、ＡからＸが５㎝、ＣからＸが６㎝です。
点ＰはＤを出発し、Ａ、Ｂを通りＣへ向かって進みます。点ＱはＢを出発し、Ｃ、Ｄを通りＡへ向かって進みます。
(１)の解説はコチラから
(２) ２点Ｐ、Ｑが同時に出発し、Ｐは毎秒１㎝、Ｑは毎秒２㎝で進むとき、出発してから１０秒後までの間で、ＰからＸまでの最短の道のりが、ＱからＸまでの最短の道のりいかなのはいつですか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(２)
Ｑの速さが毎秒１㎝から毎秒２㎝に変わっただけなのに、ややこしさ１００％アップです(笑)
【スタート時のＰとＱ】
スタート時、次の図の青い線と紫の線の長さの差は１３－７＝６㎝ありますが、１秒ごとに青い線は１㎝ずつ短く、紫の線は２㎝ずつ長くなっていくので、その差は１秒間に１＋２＝３㎝ずつ縮まっていきます。
(画像はすべて、クリックすると拡大します)
したがって、スタートしてから６÷３＝２秒後に２つの線の長さは次の図のように等しくなり、その後しばらくは、青い線が紫の線よりも短くなっています。
【スタートしてから５秒後の話 その１】
さっきはＰＸ(青い線)がＱＸ(紫の線)よりも短かったはずなのに、ＱＸは途中で緑の線に移るため、スタートしてから５秒後には次の図のように長さが逆転しています。
というわけで、上の図の状態になる前にあったはずの「逆転ポイント」を探してみることにします。
上の図は青い線が緑の線よりも８－６＝２㎝長いのですが、時間を１秒逆戻しするごとに、青い線は１㎝ずつ長く、そして緑の線は１㎝ずつ長くなっていくので、その差は２－１＝１㎝ずつ縮まっていきます。
つまり５秒後の図から２÷１＝２秒前(つまりスタートしてから５－２＝３秒後)には、次の図のように２本の線の長さが等しくなっていたので、そのときまでは青い線が緑の線よりも長かったことが分かります。
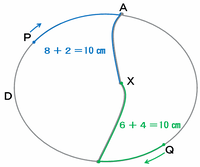
以上から、答えの範囲その１は、スタートしてから２秒後から３秒後までの１秒間になります。
【スタートしてから５秒後の話 その２】
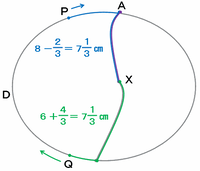
今度はスタートしてから５秒後よりも未来の話に目を向けてみると、青い線は相変わらず１秒ごとに１㎝ずつ短くなる一方、緑の線は逆に２㎝ずつ長くなっていきます。
したがって、青い線と緑の線の差である８－６＝２㎝は、１秒間に１＋２＝３㎝ずつ縮まっていきます。
ここからは分数が出てくるので、計算の式を画像に変換します。
【スタートから１２秒後の話】
なぜ１２秒後なのかというと、点Ｑがちょうど点Ａに進んでいてキリがいいからです(笑)
スタートから１２秒後、次の図のようにＱＸ(紫の線)の長さがまたＰＸ(青い線)よりも短くなっています。つまり、それよりも前に「逆転ポイント」があったはずなので、それを探す作業をしてみます。
PR
