気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
07/28
Wed
2010
淑徳与野2010【3】 ☆図形や点の移動・回転する正三角形☆
下の図のように、1辺が12㎝の正三角形アの外側に1辺が6㎝の正三角形イがあります。正三角形イを、正三角形アの辺にそって、すべらないように転がして、もとの位置まで1周させます。このとき、次の問いに答えなさい。
(1)
正三角形イがアのまわりを1周するときにできる線は、「小さなおうぎ形」と「大きなおうぎ形」の2種類に分けることができます。
【図1 小さなおうぎ形】
正三角形イがアのまわりを次の図1のように進むとき、半径6㎝で中心角120度の小さなおうぎ形が3個できます。
・ イ①のオレンジ色の点が120度回転→青い線1本目
・ イ②の緑色の点が120度回転→青い線2本目
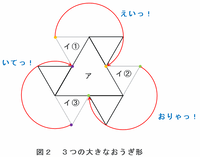
【図2 大きなおうぎ形】
正三角形イがアのまわりを次の図2のように進むとき、半径6㎝で中心角240度の大きなおうぎ形が3個できます。
・ イ①のオレンジ色の点が240度回転→赤い線1本目
・ イ②の緑色の点が240度回転→赤い線2本目
・ イ③のむらさき色の点が240度回転→赤い線3本目
【図3 青色と赤色の線を合体させてみる】
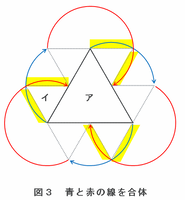
【図3 青色と赤色の線を合体させてみる】
図1と図2で確認した青色と赤色の線を合体させてみると、次の図3のようになります。
ただし、この図の黄色い6か所の曲線は、正三角形イが通るときにできる線の内側にあるので、すべて取り除いて図をスッキリさせてみます。
【図4 ついに完成】
図3の黄色い6か所の部分を削除すると、次の図のように正三角形イの外側が通った線が完成します。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
