次の図１は、図２の埼玉県章をモデルにしたものです。半円を組み合わせた図形で、ＡＢは６㎝、ＢＣは２㎝です。
※ 画像はすべて、クリックすると拡大します。
点Ｐは一定の速さでＡ→Ｓ→Ｂ→Ｃ→Ｔ→Ａの順に、点Ｑは点Ｐの３分の１の速さでＡ→Ｔ→Ｃ→Ｂ→Ｓ→Ａの順に、この図形の周上を動きます。このとき、次の問いに答えなさい。
(１)
点Ｐが点Ａを出発して点Ｂに着くまでに１０秒かかりました。点Ｐが点Ａを出発して点Ａに戻るまでに何秒かかりますか。
(２)
点Ｐと点Ｑが同時に点Ａを出発したとき、２点が出会うまでに点Ｑが動いた長さは何㎝ですか。ただし、円周率は３.１４とします。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
３つの半円を次の図のように青、緑、オレンジの３つに色分けし、点Ｐがそれぞれの半円を通過するのに何秒かかるのかを求めてみます。
※ 画像はすべて、クリックすると拡大します。
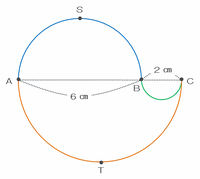
次の図の青い半円は直径６㎝、緑色の半円は直径２㎝なので、緑色の半円の直径は青い半円の直径の２÷６＝３分の１倍です。
直径が３分の１倍なら孤の長さも３分の１倍のはずなので、点Ｐが緑色の孤を通過する時間は、青色の孤を通過する時間の３分の１になります。
点Ｐが青色の孤を通過するのにかかる時間は１０秒なので、緑色の孤を通過するのにかかる時間は１０÷３＝３分の１０秒です。
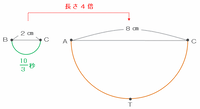
次の図のオレンジ色の半円の直径は緑色の半円の直径の８÷２＝４倍なので、オレンジ色の孤は緑色の孤の長さの４倍になります。
点Ｐは緑色の孤を３分の１０秒かけて通過するので、オレンジ色の孤を通過するのにかかる時間は３分の１０×４＝３分の４０秒になります。
つまり、点Ｐは青色の孤を１０秒、緑色の孤を３分の１０秒、そしてオレンジ色の孤を３分の４０秒かけて通過するので、点Ａを出発して再び点Ａに戻るまでに１０＋３分の１０＋３分の４０＝３分の８０秒かかります。
(２)
点Ｑの進む速さは点Ｐの３分の１なので、２つの点の速さの比はＰ：Ｑ＝１：３分の１＝３：１です。
つまり次の図のように、２つの点が同じ時間に進む距離の比もＰ：Ｑ＝３：１になるので、２つの点がＡを出発してから出会うまでに進む距離は、点Ｐがコース全体の４分の３、そして点Ｑはコース全体の４分の１になるはずです(比例配分)。
コース全体は直径２㎝、６㎝、８㎝の半円の孤の長さを合計すれば求められるので、(２＋６＋８)×３.１４÷２＝８×３.１４㎝です。
点Ｑが動いた長さはその４分の１にあたるので、答えは８×３.１４÷４＝２×３.１４＝６.２８㎝になります。
PR
