次の図のような平行四辺形と固定された長方形があります。次の図の位置から平行四辺形を毎秒０.５㎝の速さで、直線ＡＢ上を矢印の方向へ動かします。平行四辺形と長方形の重なる共通部分について、次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
共通部分が四角形であるのは、全部で何秒間ですか。
(２)
動かし始めてから２８秒後の共通部分の面積は( ア )㎠で、３２秒後の共通部分の面積は( イ )㎠です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは次の図１から図８を見て、平行四辺形が右へと進むにつれて重なりの部分(オレンジ色)の形がどのように変わっていくのかを確認してみます。
上の図を見れば分かるように、重なりの部分は「三角形→四角形→五角形→六角形→五角形→四角形→三角形」の順に変化していきます。
つまり、重なりの部分が四角形になるのは、
① 三角形から四角形になり、五角形になる直前まで(下の図９)
② 五角形から四角形になり、三角形になる直前まで(下の図１０)
の２通りが考えられます。
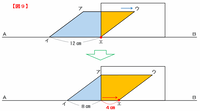
上の２つの図を見れば分かるように、どちらの場合も赤い点が４㎝動く間は重なりの部分が四角形になっています。
平行四辺形は毎秒０.５㎝で動くので、重なりの部分が四角形になる時間の合計は４÷０.５×２＝１６秒間になります。
※ 図９と図１０でそれぞれ４÷０.５＝８秒ずつあるので、合わせて８×２＝１６秒。
(２)のア
２８秒間で平行四辺形は０.５×２８＝１４㎝動くので、重なりの部分は次の図のような六角形になっています。
大まかに言えば、上の図の平行四辺形アイエウから青い三角形の面積を引けばオレンジ色の部分の面積が分かるので、まずは青い三角形の面積から求めてみます。
また、そのときにカギとなるのが、次の図(スタート時)の平行四辺形と長方形との間にできている緑色の三角形です。
この三角形は、底辺と高さの比が８㎝：６㎝＝４：３になっているのですが、これと相似の関係にある三角形を利用して問題を解いていきます。
次の図の三角形ウエキはスタート時にできる緑色の三角形と合同なので、辺エキの長さは８㎝です。
また、辺カキの長さは１４㎝なので、辺カエは１４－８＝６㎝、そして辺イカの長さは１２－６＝６㎝になります。
※ 辺イカの長さ＝辺イエ－辺カエ＝１２－６＝６㎝
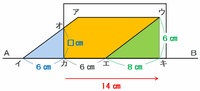
上の図の青い三角形オイカは緑色の三角形と相似なので、底辺と高さの比は４：３になっています。
辺オカの長さを□㎝とおくと、４：３＝６㎝：□㎝と表せるので、辺オカの長さは３×６÷４＝４.５㎝になります。
つまり、平行四辺形アイエウの面積は１２×６＝７２㎠、青い三角形オイカの面積は６×４.５÷２＝１３.５㎠なので、オレンジ色の部分の面積は７２－１３.５＝５８.５㎠になります。
(２)のイ
まずは３２秒後の図から確認してみると、平行四辺形は０.５×３２＝１６㎝動くので、次の図のように平行四辺形の頂点ウが長方形よりも１６－１５＝１㎝飛び出した状態になっています。
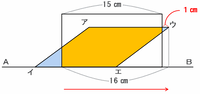
ちょっとややこしいですが、次の図の平行四辺形アイエウから赤色と青色の三角形の面積を引けば、オレンジ色の部分の面積が求められます。
【赤い三角形の面積を求める】
上の図の赤い小さな三角形も緑色の三角形と相似なので、底辺と高さの比は４：３になっています。
赤い三角形の高さを□㎝とおくと、４：３＝１㎝：□㎝という比に表せるので、高さは３×１÷４＝０.７５㎝になります。
したがって、赤い小さな三角形の面積は１×０.７５÷２＝０.３７５㎠になります。
【青い三角形の面積を求める】
下の図の辺カキは平行四辺形が３２秒間で進んだ長さなので１６㎝、辺エキは緑色の三角形の底辺なので８㎝です。
したがって、辺カエの長さは１６－８＝８㎝になります。
また、辺イカの長さは辺イエ(平行四辺形の底辺)から辺カエの長さを引けば求められるので、１２－８＝４㎝になります。
青い三角形の高さを△㎝とおくと、４：３＝４㎝：□㎝と表せるので、高さは３㎝だと分かります。
したがって、青い三角形の面積は４×３÷２＝６㎠になります。
平行四辺形アイエウの面積は７２㎠、青い三角形の面積は６㎠、赤い三角形の面積は０.３７５㎠なので、オレンジ色の部分の面積は７２－(６＋０.３７５)＝６５.６２５㎠になります。
PR
