次の図のように３つの半円で囲まれた図形の面積を、Ａを通る直線で２等分しました。角アの大きさは何度ですか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
この問題には円周率がどこにも書かれていませんが、問題を作った人がそれを忘れるうっかりさんだったわけではありません(笑)
カンタンに言えば、これは問題製作者からの「円周率を使わずに解けるんだよー」というメッセージなので、計算の途中で３.１４倍するのはやめておきましょう。
まずは半径２０㎝と半径１０㎝の半円の面積を求める式をそれぞれ書いてみると、
・半径２０㎝の半円→２０×２０×３.１４÷２
・半径１０㎝の半円→１０×１０×３.１４÷２
となります。
この２つの式にはどちらも「×３.１４÷２」があるので、その部分を消去して２つの半円の面積比を求めてみると、下の図のように２０×２０：１０×１０＝４００：１００＝④：①と表せます。
※ 画像はすべて、クリックすると拡大します。
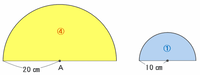
問題文のひとだまみたいな形をした図形の面積は、半径２０㎝の半円から半径１０㎝の半円を切り取って下にくっつけてできた形なので、その面積は④－①＋①＝④のままです。
また、下の図の青い直線はひとだまの面積を２等分しているので、直線の左右の面積はどちらも④÷２＝②となっています。
このとき、青い直線の左側には半径１０㎝の半円(面積は①)があるので、おうぎ形ＡＢＣの面積は②－①＝①であることが分かります。
つまり、下の図のおうぎ形ＡＢＣの面積である①は、半径２０㎝の半円の面積である④の４分の１にあたるので、中心角アの大きさは１８０÷４＝４５度になります。
PR
