辺の長さと角の大きさが、どれも等しい多角形を正多角形といいます。次の問いに答えなさい。
(１)
次の図のように、１辺の長さが等しい正八角形と正三角形があります。いま正八角形の「辺あ」と正三角形の「辺ア」が重なっていて、正三角形が正八角形の内側を左回りに辺が重なるように転がっていきます。
※ 画像はクリックすると拡大します。
１回だけ転がすと図の「辺い」と「辺イ」が重なります。また、最初の「辺あ」と「辺ア」の重なりは、重なっている回数には数えないことにします。
① 正三角形を８回転がすと正八角形の内側を１周して元の位置に戻りますが、「辺ア」は正八角形の辺と何回重なりましたか。
② 「辺ア」が正八角形のすべての辺と重なるには、正八角形の内側を最低何周しますか。
(２)
(１)と同じように正七角形の内側で正方形を転がすとき、正方形の１つの辺「辺ア」が正七角形の辺すべてと重なるには正七角形の内側を最低何周しますか。
(３)
(１)と同じように正２１０角形の内側で、ある正多角形を何回か転がすと正多角形の１つの辺「辺ア」が正２１０角形の辺とすべて重なるとき、辺の数が最も少ないものは正何角形ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)の①
正三角形が「辺あ」から左回りに１周するとき、正八角形と重なる辺は次の図のように「イ→ウ→ア」の順番の繰り返しになります。
※ 画像はすべて、クリックすると拡大します。
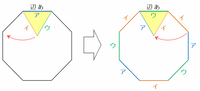
８÷３＝２余り２なので、正三角形は正八角形の内側で「イ→ウ→ア」の順を２回繰り返して転がった後、最後に「イ→ウ」と転がって最初の位置に戻ります。
したがって、辺アは正八角形の内側と２回重なりました。
(１)の②
正三角形は「イ→ウ→ア」の順に正八角形の内側をコロコロと転がり続けるので、辺アが正八角形の辺と重なるのは３回に１回であることが分かります。
また、８と３の最小公倍数は２４なので、正三角形がコロコロと２４回転がったとき、スタートのときと同じ図に戻ります。
辺アが３回に１回のペースで正八角形の辺と重なるとき、８本の辺すべてに重なるには正三角形が３×８＝２４回転がればＯＫです。
正八角形の内部を８回転がると１周するので、２４回転がったときは２４÷８＝３周になります。
【補足】
「そんな風に文章と式だけで説明されてもよく分からん」という場合は、次の図を①から④の順に見てなんとなくイメージしてお楽しみください。
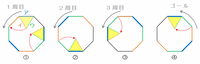
上の図の青くて太い線は、正三角形の辺アが正八角形の辺と重なったところを表しています。
８と３の最小公倍数は２４なので、２４÷８＝３周するまでは辺アが同じ場所と重ならないことがポイントです。
(２)
正七角形の内部を正方形が次の図のようにコロコロと転がっていくとき、正方形の辺は「イ→ウ→エ→ア」の順に正七角形の辺と接していきます。
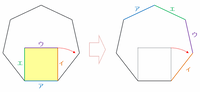
つまり、正方形の辺アは４回に１回の割合で正七角形の辺と接するので、７本の辺すべてと接するためには、正七角形の内部を４×７＝２８回コロコロと転がればＯＫです。
正七角形の内部を７回コロコロと転がればちょうど１周するので、２８回コロコロと転がったときは２８÷７＝４周しています。
※ ２８は７と４の最小公倍数であることがポイントです。さっきの問題では８と３の最小公倍数である２４回コロコロと転がればＯＫでしたね。
(３)
例えば正三角形が正２１０角形の内部をコロコロと転がる場合、３と２１０の最小公倍数は２１０なので、２１０回コロコロと転がったゴール地点は次の図のようにスタート地点と同じになります。
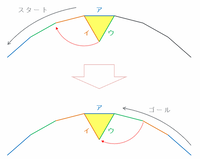
すると、２周目も辺アは１周目と同じ辺に重なるので、上の図で辺イやウが重なった辺に、辺アが重なることは永遠にありません。
「じゃあ正方形ならいけるんじゃないの？」と思うかもしれませんが、２１０と４の最小公倍数は４２０、４２０÷２１０＝２なので、正方形が正２１０角形の内部をコロコロと２周したときのゴール地点がスタート地点と同じになってしまいます。
その場合、辺アが１周目と２周目に重なった場所は違うのですが、３周目に重なる辺は１周目と同じになり、４周目に重なる辺は２周目と同じになるため、最初の２周で辺アが重ならなかった辺は、その後に何周しても永遠に重なることはありません。
このまま「正五角形は？」とか「正六角形は？」と探していけばそのうち見つかるとは思うのですが、それだと時間がかかり過ぎて困るので、(１)と(２)で分かったことを参考にして答えを見つけてみます。
さっきの２つの問題で、
・正八角形の内部を正三角形が転がる場合→転がる回数は８と３の最小公倍数である２４回
・正七角形の内部を正方形が転がる場合→転がる回数は７と４の最小公倍数である２８回
となることが分かりました。
つまり、正２１０角形の内部を正□角形が転がるときも、２１０と□の最小公倍数が「２１０×□」となる場合を見つければＯＫなので、次の連除法の図の△にあてはまる最小の数を考えてみます。
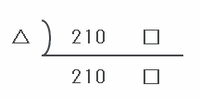
上の図の△に１があてはまれば、２１０と□の最小公倍数は１×２１０×□＝２１０×□となるので条件を満たします。
そこで、上の図の□に数をあてはめて、△＝１となる場合を探してみると・・・
・□に２の倍数をあてはめる→△には２があてはまるので×
・□に３の倍数をあてはめる→△には３があてはまるので×
・□に５の倍数をあてはめる→△には５があてはまるので×
・□に７の倍数をあてはめる→△には７があてはまるので×
となるので、１から１０までの整数はすべてアウトになります。
でも、上の図の□に１１をあてはめたときは、△に１があてはまるので、最小公倍数は１×２１０×１１＝２３１０となり、問題文の条件を満たします。
以上から、条件を満たす最小の正多角形は正１１角形になります。
※ つまり、正２１０角形の内部を正１１角形がコロコロと２３１０回転がったとき、辺アが正２１０角形のすべての辺と接します。
また、２３１０回目に転がったときの辺アの場所は、スタート地点と同じになります。
PR
